Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-07-08T02:08:54.945Z Has data issue: false hasContentIssue false
  • English
  • Français

XIV.—The Minimum System of Two Quadratic Forms in n Variables

Published online by Cambridge University Press:  15 September 2014

H. W. Turnbull  and
J. Williamson
H. W. Turnbull
Affiliation:
University of St Andrews
J. Williamson
Affiliation:
University of St Andrews
Get access

Extract

The following pages deal with the simultaneous system of two general quadratic forms in n homogeneous variables. It is a special case of Gordan's Theorem which proves such systems to be finite, for the general projective group of linear transformations. While several works have dealt with the cases when n = 2, 3, or 4, nothing seems to have been written on the general case except a memoir in the year 1908. We continue, and simplify, the results there obtained, and now establish that

(1) All rational integral concomitants of two quadratic forms in n variables and any number of sets of linear variables may be expressed as rational integral functions of (3n + 1) concomitants, and forms derivable by polarisation.

(2) These (3n + 1) forms, called the H system, constitute a strictly irreducible system.

This system is exhibited in §7 as

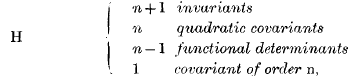
together with polars.

The work is divided into three chapters: I §§ 1–4 is introductory notation, II §§ 5–17 provides a proof of these theorems, while III §§18–21 gives the non-symbolic and canonical forms of the results.

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 45 , Issue 2 , 1926 , pp. 149 - 165
Copyright
Copyright © Royal Society of Edinburgh 1926

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 149 note * Hilbert, , Math. Ann., xxxvi (1890), p. 473 CrossRefGoogle Scholar; Grace and Young, Algebra of Invariants.

page 149 note † Hilbert, , Math. Ann., xxxvi (1890), p. 161 Google Scholar, also pp. 274–286.

page 149 note ‡ Turnbull, , Proc. London Math. Sec. (2), xviii (1919), pp. 69–91 Google Scholar.

page 149 note § Turnbull, , Trans. Camb. Phil. Soc., xxi (1909), pp. 197–240 Google Scholar.

page 150 note * Clebsch, , Göttinger Nachrichten, xvii (1872); Weitzenböck, Invariantentheorie, pp. 148–159, Groningen (1923)Google Scholar.

page 151 note * Clebsch, , Crelle, lix (1861)Google Scholar; Weitzenböck, Wiener Berichte, cxxii (1913); Grace and Young, Algebra of Invariants.

page 157 note * This is permissible as the suffix is simply a distinguishing mark and does not denote currency.

page 159 note * This method is only safe after proving that a canonical form exists which involves the same number of constants. Otherwise it may lead to a downright error. We here assume the well-known result that the two general quadratic forms can be expressed simultaneously each as the sum of n squares.

page 159 note † Gilham, , Proc. London Math. Soc. (2), xx (1921), p. 326 Google Scholar.