Published online by Cambridge University Press: 15 September 2014
The theory of mass action leads to very simple consequences when applied to the determination of the velocity of chemical processes which take place in homogeneous solution. If the reaction is pure and irreversible, the initial concentrations of the reacting substances have only to be known in order to obtain an expression which shall give for every value of the time (measured from the beginning of the reaction) the corresponding extent to which the action has taken place, one constant being involved. This constant, which is characteristic of the reaction, is called its velocity constant, and for a given medium and a given temperature is invariable. Reactions have been classified by Van't Hoff into unimolecular, bimolecular, trimolecular, etc., reactions, according to the number of molecules which interact; and to every class there corresponds an equation by means of which the velocity constant is determined, the expressions for the constants differing from each other in form from class to class. For example, if the initial concentration of each of the reacting substances be A, the time t, and z the extent to which the action has progressed at the end of the time t, then the following expressions will be constant:—
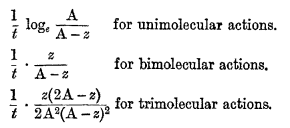
page 23 note * Phil. Mag., 5th series, vi. 371Google Scholar; viii. 121, Cf. also Noyes, and Wason, , Zeitschrift für physikalische Chemie, xxii. 210Google Scholar.
page 25 note * Phil. Trans., clvi. 216, 1866Google Scholar.