No CrossRef data available.
Article contents
On the Resolution of Circulants into Rational Factors
Published online by Cambridge University Press: 15 September 2014
Extract
(1) If we think of the circulant C(a1, a2,…., an−1, an) as the result of the elimination of x from the equations
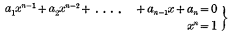
it is readily apparent that, corresponding to every rational factor of xn – 1, there must be a rational factor of the circulant. Thus the circulant of the 6th order
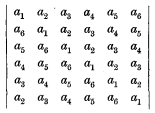
must have four rational factors, viz., the factor
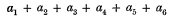
corresponding to the solution x = 1 of the equation x6 = 1, the factor
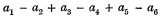
corresponding to the solution x = − 1, and two other factors corresponding to the partial equations
x2+x+1 = 0, x2−x+1 = 0.
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1897
References
* For further details regarding the co-factor of a 1 + a 2+ … + an, in the case where n is odd, a paper on “Circulants of Odd Order” may be consulted in the Quart. Journ. of Math., xviii. pp. 261–265Google Scholar.


