Article contents
Extract
1. In a paper “On the Existence of a Root of a Rational Integral Equation,” published in the Proc. Lond. Math. Soc., xxv. pp. 173–184, the author, Professor E. B. Elliott, says (p. 184) that it is unfortunate, for the simplicity of the argument of his paper, that a proof of a certain property of this eliminant, viz., that when two linear factors have been withdrawn from it, there is left a perfect square—“is one which direct algebraical methods have not yet supplied.”
In the course of the following year the want referred to received attention, a demonstration being given by Mr W. W. Taylor, in a paper entitled “Evolution of a certain Dialytic Determinant,” which was read before the same Society (see Proc. Lond. Math. Soc., xxvii. pp. 60–66).
I purpose here giving another demonstration, which I think has the merit of bringing out more clearly the character of the constitution of the eliminant, and in which is followed, at the same time, that direct and expeditious course most likely to be taken by a student familiar with the theory of determinants.
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1897
References
* See the theorem regarding centro-symmetric determinants in Scott's Textbook, pp. 68, 69; or Muir's, pp. 183, 184. The original source is Zehfuss, , Zeitsch.f. Math. u. Phys., vii. pp. 438, 439Google Scholar, where, however, the case for odd-ordered determinants is quite erroneously stated.
- 1
- Cited by


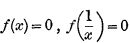 .
.