No CrossRef data available.
Published online by Cambridge University Press: 15 September 2014
It appears to me that the form in which the definition or condition of uniform convergence is usually stated, is (to say the least) not easily intelligible. I call to mind the general notion : We may have a series, to fix the ideas, say of positive terms
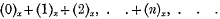
the successive terms whereof are continuous functions of x, for all values of x from some value less than a up to and inclusive of a (or from some value greater than a down to and inclusive of a): and the series may be convergent for all such values of x, the sum of the series øx is thus a determinate function øx of x; but øx is not of necessity a continuous function; if it be so, then the series is said to be uniformly convergent; if not, and there is for the value x = a a breach of continuity in the function øx then there is for this value x = a a breach of uniform convergence in the series.