If the positive integral powers of 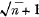be taken, and the expansion of each be separated into two parts, rational and irrational, thus—

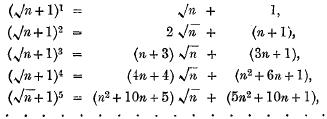
then the ratio of the rational portion to the coefficient of 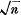in the other portion is approximately equal to 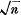, the convergence being perfect when the power of the binomial is infinite. This is the simplest case of a theorem discovered by the late Dr Sang, and enunciated by him as the result of a process of induction in his paper “On the Extension of Brouncker's Method to the Comparison of several Magnitudes” (Proc. Roy. Soc. Edin., vol. xviii. p. 341, 1890–91).