Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Birge, Raymond T.
and
Weinberg, J. W.
1947.
Least-Squares' Fitting of Data by Means of Polynomials.
Reviews of Modern Physics,
Vol. 19,
Issue. 4,
p.
298.
Cochrane, D.
and
Orcutt, G. H.
1949.
Application of Least Squares Regression to Relationships Containing Auto-Correlated Error Terms.
Journal of the American Statistical Association,
Vol. 44,
Issue. 245,
p.
32.
Box, G. E. P.
and
Wilson, K. B.
1951.
On the Experimental Attainment of Optimum Conditions.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 13,
Issue. 1,
p.
1.
Rushton, S.
1951.
On Least Squares Fitting by Orthonormal Polynomials Using the Choleski Method.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 13,
Issue. 1,
p.
92.
Sard, Arthur
1952.
Approximation and variance.
Transactions of the American Mathematical Society,
Vol. 73,
Issue. 3,
p.
428.
Vajda, S.
1953.
Theorems Relating to Quadratic Forms and their Discriminant Matrices.
Proceedings of the Edinburgh Mathematical Society,
Vol. 10,
Issue. 1,
p.
13.
Durbin, J.
1953.
A Note on Regression When There is Extraneous Information About One of the Coefficients.
Journal of the American Statistical Association,
Vol. 48,
Issue. 264,
p.
799.
Cohen, E. Richard
1953.
The Basis for the Criterion of Least Squares.
Reviews of Modern Physics,
Vol. 25,
Issue. 3,
p.
709.
Anderson, R. L.
1954.
The Problem of Autocorrelation in Regression Analysis.
Journal of the American Statistical Association,
Vol. 49,
Issue. 265,
p.
113.
Eyeions, D A
Owen, B G
Price, B T
Wilson, J G
Hammersley, J M
and
Morton, K W
1955.
The Ionization Loss of Relativistic -Mesons in Neon.
Proceedings of the Physical Society. Section A,
Vol. 68,
Issue. 9,
p.
793.
Wise, J.
1956.
Regression Analysis of Relationships between Autocorrelated Time Series.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 18,
Issue. 2,
p.
240.
Blum, M.
1956.
An extension of the minimum mean square prediction theory for sampled input signals.
IEEE Transactions on Information Theory,
Vol. 2,
Issue. 3,
p.
176.
Cohen, E. R.
1957.
Mathematical analysis of the universal physical constants.
Il Nuovo Cimento,
Vol. 6,
Issue. S1,
p.
110.
Dumond, Jesse W. M.
1958.
Present Status of Precise Information on the Universal Physical Constants. Has the Time Arrived for Their Adoption to Replace Our Present Arbitrary Conventional Standards?.
IRE Transactions on Instrumentation,
Vol. I-7,
Issue. 3/4,
p.
136.
Thell, H.
and
Kloek, T.
1959.
The statistics of systems of simultaneous economic relationships*.
Statistica Neerlandica,
Vol. 13,
Issue. 1,
p.
65.
Janos, W.
1960.
Analytic inversion of a class of covariance matrices.
IEEE Transactions on Information Theory,
Vol. 6,
Issue. 4,
p.
477.
Jorgenson, Dale W.
1961.
Multiple Regression Analysis of a Poisson Process.
Journal of the American Statistical Association,
Vol. 56,
Issue. 294,
p.
235.
1961.
Fatigue Testing and Analysis of Results.
p.
250.
Fisk, P. R.
1961.
Estimation of Location and Scale Parameters in a Truncated Grouped Sech Square Distribution.
Journal of the American Statistical Association,
Vol. 56,
Issue. 295,
p.
692.
Zellner, Arnold
1962.
An Efficient Method of Estimating Seemingly Unrelated Regressions and Tests for Aggregation Bias.
Journal of the American Statistical Association,
Vol. 57,
Issue. 298,
p.
348.
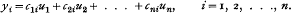
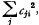 which measures the mean square error of yi, is to be a minimum for each value of i.
which measures the mean square error of yi, is to be a minimum for each value of i.