No CrossRef data available.
Published online by Cambridge University Press: 15 September 2014
(1) The main specialty in the construction of the arrays in question is that the elements of each row are the coefficients of the powers of x in the expansion of a product of the form
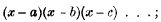
that is to say, the rows all belong to the type

The variables from which the elements of any row are formed are n − 1 consecutive members of a series of n(n − 1) members, the member considered to be consecutive to the last being the first member; for example, when n is 3 and the 3(3 − 1) independent variables are
a, b, c, d, e, f,
the rows of the arrays are
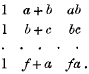
Further, these rows in order are taken to form all the first rows of the arrays, then all the second rows, and so on.