Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T12:08:00.984Z Has data issue: false hasContentIssue false
  • English
  • Français

III.—On Fourier Constants

Published online by Cambridge University Press:  15 September 2014

E. T. Copson
Get access

Extract

§ 1. Notation.—Suppose that a0, a1a2,… are real constants, such that, for some fixed p (≥1), the series 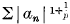is convergent. It is a consequence of the generalised Riesz-Fischer Theorem that there exists a function f(t) L1+p over ( – 1 , 1), of which

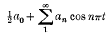
is the Fourier Series.

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 48 , 1929 , pp. 15 - 19
Copyright
Copyright © Royal Society of Edinburgh 1929

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 15 note * Hobson, Functions of a Real Variable (2nd ed.), 2, 599, Theorem II.

page 15 note † That an(l) and bn(l) exist follows from the use of Hölder's inequality for integrals, and the fact that f(t) is L1+p over (0, 1) and therefore over (0, l).

page 15 note ‡ Hobson, loc. cit., 575.

page 16 note * Hobson, loc, cit., 599.

page 16 note † Math. Ann., 97 (1926), 159–209Google Scholar.

page 16 note ‡ Math. Zeit., 25 (1926), 321–347CrossRefGoogle Scholar.

page 17 note * Hobson, loc. cit., 614 (§ 399).

page 18 note * By Minkowski's inequality.

page 18 note † By Hölder's inequality.