Article contents
XXIII.—On some Persymmetric Determinants
Published online by Cambridge University Press: 15 September 2014
Extract
We consider in this paper the persymmetric determinants
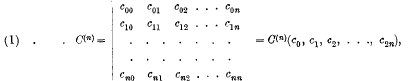
where
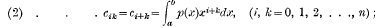
p(x) being a function which is not negative in the interval (a, b) (finite or infinite); we suppose further that the integrals
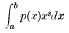
exist for s = 0, 1, 2,….
The object of this paper is the application of a theorem stated by the writer in the paper “Sur un déterminant de Hankel” to many determinants of the type (1), referred to by Sir Thomas Muir in his paper “The theory of persymmetric determinants from 1894 to 1919.”
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1931
References
page 304 note * Annais da Faculdade de Sciências do Porto (1929), t. xvi, N. 1, p. 25.
page 304 note † Proceedings of the Royal Society of Edinburgh (1926–27), vol. xlvii, part i, pp. 11–33.
page 305 note * J. Geronimus, loc. cit., p. 28.
page 305 note † Shohat, J., “A simple method for normalizing Tchebycheff polynomials,” Bulletin of the American Mathematical Society (1927), p. 431.Google Scholar
page 305 note ‡ Whittaker, E. T. and Watson, G. N., A Course of Modern Analysis (1927), p. 264.Google Scholar
page 305 note § Composto, S., “Sui determinanti ‘Wronskiani fattoriali,’” Giornale di Matematica (1919), pp. 22–30.Google Scholar
page 306 note * Muir, T., “The persymmetric determinants whose elements are in harmonical progression,” Messenger of Mathematics (1906), pp. 85–93.Google Scholar
page 306 note † G. Polya und G. Szegö, Aufgaben und Lehrsätze aus der Analysis, Bd. ii, SS. 94, 294.
page 307 note * Hilbert, D., “Ein Beitrag zur Theorie des Legendreschen Polynoms,” Acta Mathematica (1894), SS. 155–160.CrossRefGoogle Scholar
page 307 note † Dingler, H., “Über eine Determinante,” Archiv der Mathematik und Physik (1910), SS. 264–267.Google Scholar
page 307 note ‡ S. Composto, loc. cit.
page 307 note § Muir, T., “Note on unimodular and other persymmetric determinants,” Transactions of the Royal Society of South Africa (1919), pp. 95–100.CrossRefGoogle Scholar
page 308 note * Szegö, G., “Über die Entwickelung einer analytischen Funktion nach den Polynomen eines Orthogonalsystems,” Mathematische Annalen (1920), Bd. lxxxii. S. 207.Google Scholar
page 308 note † If we reduce our interval to (−1, +1) and suppose that p(−x) = p(x), then
Cf. J. Geronimus, “On a set of polynomials,” Annals of Mathematics (in the press).
page 309 note * Petr, K., “O determinantu z Bernoulliskych funkci,” Časopis pro pěstováni math, a fys. (1903), pp. 9–12.Google Scholar
page 309 note † Tchebycheff, P., “Sur l'interpolation,” Œuvres, t. i, pp. 547, 552.Google Scholar
- 1
- Cited by


