The elliptic cylinder functions, or solutions of the Mathieu equation

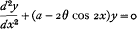
that have the period π or 2π, are of four distinct species. These are denoted respectively by ce2n(x, θ), se2n+1 (x, θ), ce2n+1 (x, θ), se2n+2(x, θ), where n indicates the number of zeros in the open interval o < x < ½π. The object of this paper is to show that a function of any type can be expressed in terms of functions of other types, or of their derivatives. This provides the analogies to such trigonometrical relations as

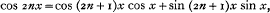
but the single terms on the right-hand side of this and similar relations are replaced, in the results to be proved, by infinite series. These results are quite distinct from Whittaker's recurrence-relations (Journ. London Math. Soc., vol. iv, 1929, pp. 88–96); in particular, they do not involve the non-periodic second solutions.