No CrossRef data available.
Published online by Cambridge University Press: 15 September 2014
1. The theorem which expresses the product of two determinants as a sum of like products is the main instrument for investigating the relations between the determinants of an oblong array. It is justifiably spoken of as “Sylvester's theorem of 1839 and 1851,” although simple cases of it date back to far earlier times; for example, the case
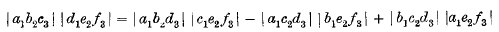
which was brought to light by Bezout in 1779.
page 219 note * A curious fate has attended this theorem of recent years. Although it is of fundamental importance, and used to be so considered by the earlier writers of text-books like Brioschi and Baltzer, we have the unfortunate fact now facing us that no mention of it is made in any of the students' manuals at present on sale by publishers throughout the world. For proof see Scott in English, Pascal in Italian, Kowalewski in German, and Dostor in French.
page 224 note * Pascal, E., Sui determinanti gobbi a matrici. Rendic. … Accad. … di Napoli (3), xxiii, pp. 40–47.
Notwithstanding this paper it would still seem a most natural and simple way of treating Voigt's determinant (1) to make the odd-numbered rows occupy the 1st, 2nd, 3rd, … places and to reverse the order of the remaining rows, (2) to do the same in the case of the columns, (3) to multiply the displaced rows by ![]() and the displaced columns by
and the displaced columns by ![]() , and (4) to use Zehfuss' theorem on the centrosymmetric determinant thus resulting.
, and (4) to use Zehfuss' theorem on the centrosymmetric determinant thus resulting.