Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-19T06:01:33.495Z Has data issue: false hasContentIssue false
  • English
  • Français

X.—On the Invariance of Quantized Field Equations

Published online by Cambridge University Press:  15 September 2014

K. Fuchs
K. Fuchs
Affiliation:
University of Edinburgh
Get access

Extract

Heisenberg and Pauli (1929) developed a general scheme for the quantization of a field, if the field equations can be derived from a variation principle,

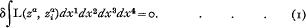
Here za denotes the field variables, L is the Lagrangian, and

The scheme of Heisenberg and Pauli is known to be Lorentz invariant. It is the purpose of this paper to show that it is also invariant with regard to all co-ordinate transformations allowed by the general theory of relativity. The method adopted to prove this is that used by Infeld (1937) and Pryce (1937) to prove the invariance of the “New Field Equations” against Lorentz transformations.

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 59 , 1940 , pp. 109 - 121
Copyright
Copyright © Royal Society of Edinburgh 1940

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

Heisenberg, W., and Pauli, W., 1929. “Zur Quantendynamik der Wellen-felder,” Zeits. Phys., vol. lvi, p. 1.CrossRefGoogle Scholar
Infeld, L., 1937. “The Lorentz Transformations in the New Quantum Electrodynamics,” Proc. Roy. Soc. (A), vol. clviii, p. 368.Google Scholar
Jordan, P., 1926. “Über kanonische Transformationen in der Quantenmechanik,” Zeits. Phys., vol. xxxvii, p. 383; vol. xxxviii, p. 513.CrossRefGoogle Scholar
Nordheim, L., and Fues, E., 1927. “Die Hamilton-Jakobische Theorie der Dynamik,” Handbuch der Physik, vol. v, p. 91 (see particularly equation (5), p. 98).Google Scholar
Pryce, M. H. L., 1937. “On the New Field Theory,” Proc. Roy. Soc. (A), vol. clix, p. 355.Google Scholar
Weiss, P., 1938. “On the Hamilton-Jacobi Theory and Quantization of Generalised Electrodynamics,” Proc. Roy. Soc. (A), vol. clxix, p. 102.Google Scholar