Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T10:25:59.609Z Has data issue: false hasContentIssue false
  • English
  • Français

XI.—The Minors of a Product-Determinant

Published online by Cambridge University Press:  15 September 2014

Thomas Muir
Get access

Extract

1. If for aα+bβ+cγ+…we put

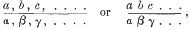
the the product of |a1b2c3| and |f1g2h3| may be written

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 27 , 1907 , pp. 79 - 87
Copyright
Copyright © Royal Society of Edinburgh 1907

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 79 note * This is usually written but throughout the present paper row-by-column multiplication is used, so as to have the results immediately applicable to matrices.

page 84 note * In the original memoir (Trans. Roy. Soc. Edin., xxxii. pp. 461–482), in which the properties of the functions which represent the elements of product-determinants are investigated, it is stated (p. 481) that they were given the name ‘bipartite’ from Cayley's use of the word for a special set of the functions, namely, those of the third degree. It has often since appeared to me that it would have been preferable to have extended the meaning of another word, namely, the word ‘cumulant,’ this being the name given by Sylvester to a special set of the second order.