Article contents
XII.—The Theory of Circulants from 1861 to 1880
Published online by Cambridge University Press: 15 September 2014
Extract
Robert's theorem concerns the circulant C whose elements are the terms of the expansion of 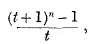
and is to the effect (1) that there are no odd powers of t in the development of the circulant, and (2) that if in the said development ξ be put for t2, the equation in ξ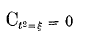
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1913
References
page no 136 note * For his mode of proof see under Baltzer (1864).
page no 137 note * Namely, by using on the first equation the multipliers x, x2,…, xn−1, and substituting 1 for xn wherever the latter turns up, exactly as Beltrami did. The same result, however, is reached by following Bezout's “abridged method.” On the other hand, the application of Sylvester's dialytic method unmodified entails, as we know, the performance of multiplication on both equations, and gives an eliminant of a higher order. For example, in the case of n = 3 it gives

where we have to increase the 4th column by the 1st, and the 5th by the 2nd, before we can reach C(a0, a2, a1).
page no 138 note * See History, ii. pp. 369 –370.
page no 138 note † He means “not greater.”
page no 141 note * A determinant which is doubly orthosymmetric can have only two different elements and must have all its odd-numbered columns identical, and all its even-numbered columns identical. This is readily seen on starting with the first two elements and then carrying out the requirements of double orthosymmetry. For example

page no 146 note * 2e3a3, 12c3bcd, 12a3def should be 2c3a3, 12a3bcd, 12c3def.
page no 146 note † This is the reason why we do not combine the two into ![]()
- 1
- Cited by


