Published online by Cambridge University Press: 15 September 2014
§ 1. Ordinary and singular periodic solutions of a dynamical system. — The present paper is concerned with the motion of dynamical systems which possess an integral of energy. To fix ideas, we shall suppose that the system has two degrees of freedom, so that the equations of motion in generalised co-ordinates may be written in Hamilton's form
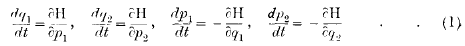
where (q1q2) are the generalised co-ordinates, (p1, p2) are the generalised momenta, and where H is a function of (q1, q2, p1, p2) which represents the sum of the kinetic and potential energies.
page 96 note * Ignoring the exceptional case of those geodesies which pass through an umbilicus.
page 96 note † This is obvious in the case when the ellipsoid is of revolution: for then the two portions of the line of curvature are parallel circles on the surface, and the ∞1 geodesies which belong to this line of curvature are obtained from each other by mere rotation about the axis of symmetry.
page 97 note * Cf., e.g., my Analytical Dynamics, § 144.
page 97 note † As this problem of motion on an ellipsoid is only a special case of the general theory which is given later. I do not sive the analysis relating to it in detail.
page 98 note * The case of geodesic problems is exceptional, as in them the value of the constant of energy is immaterial.
page 98 note † Nouvelles Méth. de la Méc. Cel., i (1892), iii (1899).
page 98 note ‡ Cf., e.g., chap. xvi of my Analytical Dynamics.
page 99 note * The only case of exception is when all the orbits of the system are periodic.
page 99 note † From ![]() brotherly, because these orbits stand in very close relation to eacli other, and also because the integral corresponding to the transformation stands in a much closer relation to the integral of energy than do the other integrals of the system.
brotherly, because these orbits stand in very close relation to eacli other, and also because the integral corresponding to the transformation stands in a much closer relation to the integral of energy than do the other integrals of the system.
page 100 note * The integral of energy corresponds to that infinitesimal transformation which changes every orbit into itself, each point of an orbit being displaced in the direction of the tangent to the orbit.
page 101 note * Cf., e.g., Analytical Dynamics, §§ 184–6.
page 106 note * Astr. Nach. 109 (1884), p. 215.
page 107 note * Cf., e.g., Analytical Dynamics, § 121.
page 108 note * Cf., e.g., Analytical Dynamics, § 121.