Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T05:19:00.693Z Has data issue: false hasContentIssue false
  • English
  • Français

VII.—On an Integral-Equation whose Solutions are the Functions of Lamé

Published online by Cambridge University Press:  15 September 2014

E. T. Whittaker
Get access

Extract

§ 1. Object of Paper.—The chief object of the present paper is to establish the following theorem:

The functions of Lamé [that is to say, the doubly-periodic solutions of the differential equation

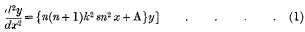
are the solutions of the homogeneous integral-equation

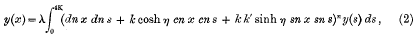
where η denotes an arbitrary constant.

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 35 , 1915 , pp. 70 - 77
Copyright
Copyright © Royal Society of Edinburgh 1915

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 71 note * Lamé's differential equation (1) when expressed in algebraic form has four regular singularities. Mathieu's differential equation

when expressed in algebraic form has two regular singularities and one irregular singularity, which latter may be regarded as formed by the confluence of two other regular singularities, making four in all. Legendre's differential equation has three regular singularities: and Bessel's equation is a confluent form of Legendre's.