No CrossRef data available.
Published online by Cambridge University Press: 15 September 2014
Projective and differential geometry are in close touch at two places, once because of the fundamental rôle played by a quaternary quadratic form in each,
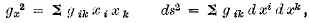
and again through the quadratic in six associated variables,
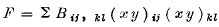
where

page 72 note * Proc. Roy. Soc. Edinburgh, 46 (1926), 210–222Google Scholar, referred to later in these pages as P.R.S.E., 46.
page 72 note † Cf. Proc. London Math. Soc., 2, 25 (1926), 303–327 (320)Google Scholar.
page 73 note * P.R.S.E., 46.
page 75 note * Turnbull, and Williamson, , Proc. Roy. Soc. Edinburgh, 45 (1925), 149–165CrossRefGoogle Scholar.
page 75 note † P.R.S.E., 46 (1926), 210–222Google Scholar.
page 79 note * Grace and Young, Algebra of Invariants, p. 322.
page 79 note † Turnbull, , Proc. London Math. Soc., 2, 9 (1910), 89–121Google Scholar.
page 80 note * P.R.S.E., 46, loc. cit., p. 215.
page 81 note * Cf. P.R.S.E., 46, p. 222.