Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Leser, C. E. V.
1961.
A Simple Method of Trend Construction.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 23,
Issue. 1,
p.
91.
Joseph, A. W.
1962.
Subsidiary Sequences for Solving Leser’s Least-Squares Graduation Equations.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 24,
Issue. 1,
p.
112.
Leser, C. E. V.
1963.
Estimation of Quasi-Linear Trend and Seasonal Variation.
Journal of the American Statistical Association,
Vol. 58,
Issue. 304,
p.
1033.
Pauly, Ralf
1989.
A general structural model for decomposing time series and its analysis as a generalized regression model.
Statistical Papers,
Vol. 30,
Issue. 1,
p.
245.
Fahrmeir, Ludwig
1995.
Grundlagen der Statistik und ihre Anwendungen.
p.
109.
Pauly, Ralf
1997.
Analyse saisonaler Zeitreihen.
Vol. 134,
Issue. ,
p.
45.
Weinert, Howard L.
2007.
Efficient computation for Whittaker–Henderson smoothing.
Computational Statistics & Data Analysis,
Vol. 52,
Issue. 2,
p.
959.
Pollock, Stephen
2008.
COMPSTAT 2008.
p.
531.
Pollock, D. S. G.
2009.
Palgrave Handbook of Econometrics.
p.
243.
Urbas, Aaron A.
and
Choquette, Steven J.
2011.
Automated Spectral Smoothing with Spatially Adaptive Penalized Least Squares.
Applied Spectroscopy,
Vol. 65,
Issue. 6,
p.
665.
Moulart, Raphaël
and
Rotinat, René
2014.
On the use of a penalized least squares method to process kinematic full-field measurements.
Measurement Science and Technology,
Vol. 25,
Issue. 7,
p.
075001.
Guerrero, Victor M.
and
Silva, Eliud
2015.
Smoothing a Time Series by Segments of the Data Range.
Communications in Statistics - Theory and Methods,
Vol. 44,
Issue. 21,
p.
4568.
Mills, T. C.
and
Patterson, K. D.
2015.
MODELLING THE TREND: THE HISTORICAL ORIGINS OF SOME MODERN METHODS AND IDEAS.
Journal of Economic Surveys,
Vol. 29,
Issue. 3,
p.
527.
Kakushadze, Zura
and
Serur, Juan Andrés
2018.
151 Trading Strategies.
p.
143.
Maidment, Alison
2021.
The Edinburgh Mathematical Laboratory and Edmund Taylor Whittaker's role in the early development of numerical analysis in Britain.
Historia Mathematica,
Vol. 55,
Issue. ,
p.
39.
Baydaroğlu, Özlem
Muste, Marian
Cikmaz, Atiye Beyza
Kim, Kyeongdong
Meselhe, Ehab
and
Demir, Ibrahim
2024.
Testing protocols for smoothing datasets of hydraulic variables acquired during unsteady flows.
Hydrological Sciences Journal,
p.
1.
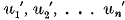 , which represent the most probable true values of the variable ux corresponding to these values of x, so that the “graduated” numbers
, which represent the most probable true values of the variable ux corresponding to these values of x, so that the “graduated” numbers 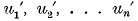 differ as little as possible from the “ungraduated” numbers u1, u2, … un, but are freed from the accidental irregularities, and thus form a “smooth” sequence, i.e. a sequence from which a regular difference-table can be formed for use in various calculations.
differ as little as possible from the “ungraduated” numbers u1, u2, … un, but are freed from the accidental irregularities, and thus form a “smooth” sequence, i.e. a sequence from which a regular difference-table can be formed for use in various calculations.