No CrossRef data available.
Published online by Cambridge University Press: 15 September 2014
Given two sets of linear homogeneous equations in n1 and n2 variables respectively
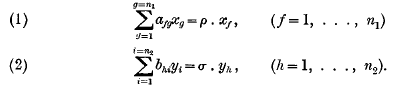
Let us form another set by multiplying every equation of (1) by every equation of (2). Thus
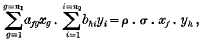
or
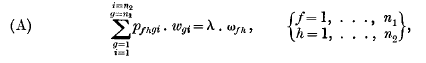
where
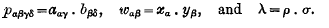
This set (A) of n=n1·n2 equations is linear and homogeneous in the n=n1·n2 variables w.
page 58 note * Metzler, Am. Math. Monthly, vol. vii, pp. 151–153 (1898–1900); cf. Moore, Annals Math., 2nd series, vol. i, pp. 177–188 (1900); Pascal, Rend. circ. Mat. Palermo, t. 22, pp. 371–382 (1906).
It may be observed here that, since R is the product of the roots of the equation in λ and is a product of powers of the roots of the equations in ρ, σ, τ …, and therefore a product of powers of the determinants A, B, … K; and since the determinants are in general irreducible and no one has prominence over another, we have another proof of I.
The case of I for k=2 is said to be due to Kronecker, and reference may be made to Jour. f. Math., Bd. 72, pp. 152–175 (1870). For other proofs, vide Hensel, Acta Math., Bd. 14, pp. 317–319 (1891); Netto, Acta Math., Bd. 17, p. 200 (1893).
page 59 note * Muir, South African Assoc. Adv. Sci., vol. i (1903); Pascal, loc. cit., 1.
Pascal in his Die Determinanten calls this the Scholtz-Hunyady determinant. It was considered by them in 1878–1880, but, as Muir points out in his paper, it was considered by Brill, Math. Annalen, Bd. 3, pp. 459–468, in 1871.
page 59 note † Metzler, Am. Jour. Math., vol. xvi, pp. 131–150 (1893); cf. Rados, Math. Annalen, Bd. 48 (1897).
page 59 note ‡ It may be observed that since R is the product of all the roots, we have another proof of IV.