^{page 652 note *} It may be well to note in passing that if π₂, π₄, π₆,…had occurred in the 3rd, 5th, 7th,…of the set of equations, respectively, the solution would have been equally simple, the only difference then being that the first column of the last determinant would have had these quantities in the 2nd, 4th, 6th,…places.

^{page 655 note *} It would have seemed more direct and natural to have shown that V₁ is transformable into the continued-fraction determinant

and therefore V₂ into the determinant got from this by deleting the first row and first column.

^{page 658 note *} This oversight runs through Sect. I., and should be corrected in the results marked (3), (4), (6), (7), (8).

^{page 659 note *} The transformation is probably most readily effected by dividing the 2nd, 3rd, 4th,….rows by

b ₁, b ₂, b ₁ b ₃, b ₂ b ₄, b ₁ b ₃ b ₅, b ₂ b ₄ b ₆, b ₁ b ₃ b ₅ b ₇,….

respectively, and multiplying the 3rd, 4th, 5th,…. columns by the same, the most instructive order of performing these operations being that in which each division is immediately followed by the corresponding multiplication. As the number of the divisions is necessarily one more than the number of multiplications, the reason for the outside factor b_nb_n–2b_n–4 …. on the left member of the identity is also thus made apparent.

^{page 660 note *} For Heine's repudiation see his Handbuch der Kugelfunction, i. (1878), pp. 261–262.

^{page 661 note *} The total number of footnote references in the book is 116.

^{page 661 note †} Zeitschrift f. Math. u. Phys., v. (1860), pp. 362–363.

^{page 663 note *} Fürstenau, E. Darstellung der reellen Wurzeln algebraischer Gleichungen durch Determinanten der Koefficienten. 35 pp., Marburg, 1860. A short but clear account of the essential parts of this pamphlet will be found in the Zeitschrift f. Math. u. Phys., vi. Liter. Zeitung, pp. 9–11.

^{page 665 note *} With the correct values for U and V as here given, it is possible to take a step farther. For it will be found that

and consequently that the continued fraction is

where the three-line determinants are the complementary minors of the elements (4, 1), (4, 2) of either of the original determinants, and where the two-line determinants are the cofactors of the last elements in the three-line determinants, and so on.

^{page 667 note *} The deletion of z ₂ where it appears in K and elsewhere as the cofactor of a two-line determinant would effect an amendment of the second part of the work, the values of K, L, M, N being then reducible to z ₂(x ₂-x ₁)|y ₁ z ₂|, z ₂(y ₂--y ₁), z ₂(z ₂-z _l)|1x ₂ y ₃|, z ₂|1 x ₂ z ₃; but there is an error in the first part as well.

The four-line determinant, which is the denominator of the fraction sought above to he expressed as a continued fraction, is really transformable into

and the four-line determinant, which is the numerator, is obtainable from this by putting 0 for x ₀, y ₀, z ₀,—a substitution which only changes the first two elements of the first column into |y ₁ z ₂,|, 0. The continued fraction thus is

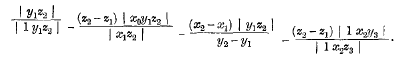
^{page 668 note *} This theorem was not published until five years afterwards. See paper entitled “General Theorems on Determinants” in Trans. R. Soc. Edinburgh, xxix. pp. 47–54.

^{page 669 note *} Some of these results and others are dealt with more fully in a pamphlet of 32 pages printed about the same time at the University Press in Glasgow, and entitled “The Expression of a Quadratic Surd as a Continued Fraction.”

^{page 671 note *} In connection herewith it may be noted that corresponding problems in the theory of continued fractions date much earlier: for example, problem No. 40 of Crelle's Journal, ii. (1827), p. 193, a solution of which is given by Th. Clausen in a paper with the title “Die Function durch die Anzahl der α ausgedrückt,” published in Crelle's Journal, iii. pp. 87–88. In our analysis of Ramus' paper of 1856 the first of the two values there given for the continued fraction is that obtained by Clausen.

^{page 676 note *} The rather noteworthy theorem in continuants which is the basis of this striking result in continued fractions can be still more widely generalised as follows:−

The continuant

is unaltered in value by adding

to the elements of the main diagonal, and changing the elements of the upper minor diagonal into

Putting in this r₁, r₂ , … = s₁, s₂, … we have the identity

and specialising further by putting each of the s's equal to s we come back to the theorem of the paper above reviewed.

^{page 677 note *} This the author reckoned as the second edition of his “Éléments” published at Mons in 1875.