Article contents
Some further Results in the Mathematical Theory of Seiches
Published online by Cambridge University Press: 15 September 2014
Extract
§ 1. In the practical calculation of the periods and nodes of the lakes we have hitherto examined it has been found that the use of the Seiche Functions gives the best results. Indeed, as will appear from details presently to be submitted to the Society by Mr E. M. Wedderburn and myself, the agreement between theory and observation, so far as we have gone, is beyond what might reasonably have been expected. Also the phenomena of concave lakes, i.e. such as have no shallows or points of minimum depth, are easily deducible from the formulæ given in an abstract (Proc. R.S.E., vol. xxv. p. 328, 6th Oct. 1904) which I communicated to the Society on 18th July 1904. On the other hand, the theory of convex lakes is less easy of manipulation, chiefly owing to the difficulty in calculating the roots of the equations 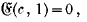
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1906
References
page 638 note * When breadth of the lake is not uniform, and the form of the cross-section varies, we must use the normal curve ; but in practice this merely requires an alteration in the meaning of the constants h and a.
page 643 note * “Essai théorique sur les Seiches,” Arch. Genève, xxv. 628, 1891.
- 9
- Cited by


