No CrossRef data available.
Article contents
On the Linear and Vector Function
Published online by Cambridge University Press: 15 September 2014
Extract
In a paper read to the Society in May last, I treated specially the case in which the Hamiltonian cubic has all its roots real. In that paper I employed little beyond the well-known methods of Hamilton, but some of the results obtained seemed to indicate a novel and useful classification of the various forms of the Linear and Vector Function. This is the main object of the present communication.
It is known that we may always write
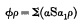
and that three terms of the sum on the right are sufficient, and in general more than is required, to express any linear and vector function. In fact, all necessary generality is secured by fixing, once for all, the values of α, β, γ, or of α1, β1, γ1, leaving the others arbitrary:—subject only to the condition that neither set is coplanar. Thus as a particular case we may write either

In either case we secure the nine independent scalar coefficients which are required for the expression of the most general homogeneous strain. But forms like these are relics of the early stage of quaternion development, and (as Hamilton expressly urged) they ought to be dispensed with as soon as possible.
2. A linear and vector function is completely determined if we know its effects on each of any system of three non-coplanar unit-vectors, say α, β, γ. If its cubic have three real roots, these vectors may, if we choose be taken as the directions which it leaves unaltered; if but one, we may take a corresponding system in the form
α, βcosa ± ιγsinα,
where ι is 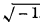 But it is preferable to keep the simpler form α, β, γ, with the understanding that β and γ may be bi-vectors, of the form just written.
But it is preferable to keep the simpler form α, β, γ, with the understanding that β and γ may be bi-vectors, of the form just written.
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1897


