No CrossRef data available.
Published online by Cambridge University Press: 15 September 2014
The problem occurs in a paper of Professor Tait's (“Glissettes of an Ellipse and of a Hyperbola,” Proc. Roy. Soc. Edin., xvii. pp. 2–4). An ellipse whose semi-axes are a and b is considered as moving so as always to be in contact with both axes of coordinates, and the glissette in question is the curve traced out during this motion by a point whose coordinates with respect to the axes of the ellipse are p and q. Professor Tait states, and it is readily seen, that if the current coordinates of the point be x and y, and θ be the variable angle made by one of the axes of the ellipse with the axis of x, we have the equations
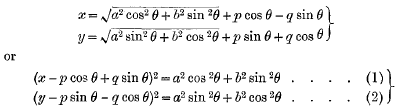
and that to obtain the x-and-y equation of the glissette it remains to eliminate θ between these two equations.