Article contents
IX.—Generalised Derivatives and Integrals*
Published online by Cambridge University Press: 15 September 2014
Extract
The various definitions which have been adopted by one or more writers for Dnf(x), where n is real but not an integer, fall roughly into three classes:—
(1) Liouville —a method which assumes a convergent expansion
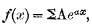
and defines Dnf(x) as ΣAαneax.
(2) Riemann, Grünwald, Laurent and others—methods which, however they begin, ultimately come to the “integral definition,”
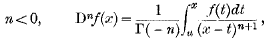
the lower limit of integration being arbitrary:
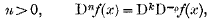
where k is a positive integer, 0<ρ<1, and n=k – ρ.
(3) Pincherle5—a method which, seeking an operator with certain properties, gives an infinite series as a definition of Dnf(x)
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1929
References
List of writings to which reference has been made
- 1
- Cited by


