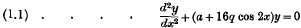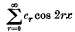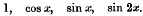Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Strutt, M. J. O.
1931.
Beugung einer ebenen Welle an einem Spalt von endlicher Breite.
Zeitschrift f�r Physik,
Vol. 69,
Issue. 9-10,
p.
597.
Strutt, M. J. O.
1932.
Lamésche - Mathieusche - und Verwandte Funktionen in Physik und Technik.
p.
110.
Strutt, M. J. O.
1932.
Lamésche — Mathieusche — und Verwandte Funktionen in Physik und Technik.
p.
110.
Koenig, Harold D.
1933.
Calculation of Characteristic Values for Periodic Potentials.
Physical Review,
Vol. 44,
Issue. 8,
p.
657.
Erdélyi, A.
1935.
Über die rechnerische Ermittlung von Schwingungsvorgängen in Kreisen mit periodisch schwankenden Parametern.
Archiv für Elektrotechnik,
Vol. 29,
Issue. 7,
p.
473.
1946.
Recent Mathematical Tables.
Mathematics of Computation,
Vol. 2,
Issue. 14,
p.
68.
Haacke, Wolfhart
1951.
Bemerkungen zur Stabilisierung eines physikalischen Pendels. I.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 31,
Issue. 6,
p.
161.
Cambi, E.
1956.
Possibility of free oscillations in a variable-parameter resonant system.
Il Nuovo Cimento,
Vol. 3,
Issue. S2,
p.
137.
YAO, JOHN C.
1963.
DYNAMIC STABILITY OF CYLINDRICAL SHELLS UNDER STATIC AND PERIODIC AXIAL AND RADIAL LOADS.
AIAA Journal,
Vol. 1,
Issue. 6,
p.
1391.
Bouwkamp, C.
1970.
Theoretical and numerical treatment of diffraction through a circular aperture.
IEEE Transactions on Antennas and Propagation,
Vol. 18,
Issue. 2,
p.
152.
de Buda, P.G.
and
Kostin, M.D.
1986.
Tunneling reactions with two reaction paths.
Chemical Physics Letters,
Vol. 127,
Issue. 3,
p.
219.
Raghavan, S
and
Kenkre, V M
1994.
Quantum mechanical bound rotator as a generalized harmonic oscillator.
Journal of Physics: Condensed Matter,
Vol. 6,
Issue. 47,
p.
10297.
Stamnes, J J
and
Spjelkavik, B
1995.
New method for computing eigenfunctions (Mathieu functions) for scattering by elliptical cylinders.
Pure and Applied Optics: Journal of the European Optical Society Part A,
Vol. 4,
Issue. 3,
p.
251.
Bezerra, V. B.
and
Rego-Monteiro, M. A.
2004.
Some boundary effects in quantum field theory.
Physical Review D,
Vol. 70,
Issue. 6,
Sorokin, V.S.
2014.
Analysis of motion of inverted pendulum with vibrating suspension axis at low-frequency excitation as an illustration of a new approach for solving equations without explicit small parameter.
International Journal of Non-Linear Mechanics,
Vol. 63,
Issue. ,
p.
1.
Sudakov, M. Yu.
and
Mamontov, E. V.
2016.
Analysis of the quadrupole mass filter with quadrupole excitation by the envelope equation method.
Technical Physics,
Vol. 61,
Issue. 11,
p.
1715.
Kovacic, Ivana
Rand, Richard
and
Mohamed Sah, Si
2018.
Mathieu's Equation and Its Generalizations: Overview of Stability Charts and Their Features.
Applied Mechanics Reviews,
Vol. 70,
Issue. 2,
Chandrasekaran, Srinivasan
and
Kiran, P. A.
2018.
Mathieu stability of offshore triceratops under postulated failure.
Ships and Offshore Structures,
Vol. 13,
Issue. 2,
p.
143.
Bai, Yang
Korwar, Mrunal
and
Orlofsky, Nicholas
2020.
Electroweak-symmetric dark monopoles from preheating.
Journal of High Energy Physics,
Vol. 2020,
Issue. 7,
Masaki, Emi
Aoki, Arata
and
Soda, Jiro
2020.
Stability of axion dark matter-photon conversion.
Physical Review D,
Vol. 101,
Issue. 4,