No CrossRef data available.
Article contents
III.—On some Problems involving the Persymmetric Determinants*
Published online by Cambridge University Press: 15 September 2014
Extract
Consider a system of “orthogonal polynomials”
P0, P1 (x), P2(x), …
possessing the property
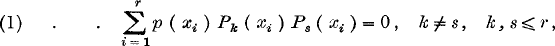
x1, x2, …, xr being real given numbers, and p (x) a given “weight” function.
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1932
References
page 15 note * Appell, P., “Sur une classe de polynomes,” Annales de l'École Normale, t. 9 (1880), pp. 119–144.CrossRefGoogle Scholar
page 16 note * Jacobi, C., “Ueber die Darstellung einer Reihe gegebener Werthe durch eine gebrochene rationale Funktion.”—Gesammelte Werke, t. iii, SS. 479–511.Google Scholar
page 17 note Brioschi, F., “Intorno ad alcune questioni d'algebra superiore,” Opere Matematiche, t. i, pp. 127–142.Google Scholar
page 17 note † Sylvester, J., “On a remarkable discovery in the theory of canonical forms and of hyperdeterminants,” Collected Mathematical Papers, t. i, pp. 265–283.Google Scholar
page 18 note * Geronimus, J., “Sur un problème d'Hermite,” Bulletin de la Classe des Sciences Physiques et Mathématiques de l'Académie des Sciences d'Ukraine, t. iv, fasc. 5 (1930), pp. 295–298.Google Scholar