No CrossRef data available.
Article contents
The Eliminant of a Set of Quaternary Quadrics
Published online by Cambridge University Press: 15 September 2014
Extract
1. The “dialytic” method of elimination, in the case of more than one variable, is not without its drawbacks, as most mathematicians know. The requisite derived equations are not always easily obtained, the difficulty being due as often to the existence of too many as of too few; and, when this has been got over, it not unfrequently happens that the order of the resulting determinant is alarmingly high, and unaccompanied by any hope of a successful guess as to the character of the extraneous factor. The discoverer's original paper affords sufficient testimony of this, and very little has been done since its appearance to put matters on a sounder footing. The most noteworthy improvement, due to Cayley, is more interesting theoretically than practically, his main object being the detection of the extraneous factor when there is an over-plus of equations. Nothing, indeed, will be found more conducive to an understanding of the limitations of the method than a careful comparison of the application of this process of Cayley's to the problem of eliminating x, y, z from the three ternary quadrics
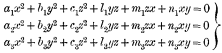
with Sylvester's original treatment of the same problem, and the latter especially as commented on in footnotes by the author himself.
2. The want of definiteness in the mode of arriving at the exact number of derived equations is not without its compensating advantage, as it leaves that scope for the exercise of ingenuity which is half the charm of mathematical work.
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1897
References
* Sylvester, , “Examples of the Dialytic Method of Elimination as applied to Ternary Systems of Equations,” Camb. Math. Journ., ii. (1841), pp. 232–236Google Scholar.
† Cayley, , “On the Theory of Elimination,” Camb. and Dub. Math. Journ., iii. (1848), pp. 116–120Google Scholar; or Collected Math. Papers, i. pp. 370–374Google Scholar.


