No CrossRef data available.
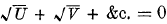
Published online by Cambridge University Press: 15 September 2014
If U, V, &c., are rational and integral functions (*) (x, y, z)r, all of the same degree r, in regard to the co-ordinates (x, y, z), then  is a polyzome, and the curve
is a polyzome, and the curve  = 0 a polyzomal curve. Each of the curves
= 0 a polyzomal curve. Each of the curves  (or say the curves U = 0, V = 0, &c.), is on account of its relation of circumscription to the curve
(or say the curves U = 0, V = 0, &c.), is on account of its relation of circumscription to the curve  , considered as a girdle thereto (ζωμα), and we have thence the term “zome” and the derived expressions “polyzome,” “zomal,” &c. If the number of the zomes
, considered as a girdle thereto (ζωμα), and we have thence the term “zome” and the derived expressions “polyzome,” “zomal,” &c. If the number of the zomes  , then we have a v-zome, and corresponding thereto a v-zomal curve; the curves U = 0, V = 0, &c., are the zomal curves or zomals thereof. Then cases v = 1, v = 2, are not, for their own sake, worthy of consideration; it is in general assumed that v is = 3 at least.
, then we have a v-zome, and corresponding thereto a v-zomal curve; the curves U = 0, V = 0, &c., are the zomal curves or zomals thereof. Then cases v = 1, v = 2, are not, for their own sake, worthy of consideration; it is in general assumed that v is = 3 at least.