Published online by Cambridge University Press: 14 February 2012
I. Introduction.—Consider a Hamiltonian system of differential equations
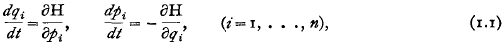
where H is a function of the 2n variables qi and pi involving in general also the time t. For each given Hamiltonian function H the system (1.1) possesses infinitely many absolute and relative integral invariants of every order r = 1,…, 2n, which can all be written out when (1.1) is integrated. Our interest now is not in these integral invariants, which are possessed by one Hamiltonian system, but in those which are possessed by all Hamiltonian systems. Such an integral invariant, which is independent of the Hamiltonian H, is said to be universal.
page 237 note * For r = 1, see Whittaker, E. T., Analytical Dynamics, 2nd ed., § 117.Google Scholar For any r, see Goursat, E., Leçons sur le problème de Pfaff, p. 214Google Scholar.
page 237 note † , Whittaker, l.c., p. 272.Google Scholar
page 237 note ‡ , Goursat, l.c., p. 231.Google Scholar
page 237 note § This follows from a known theorem (, Goursat, l.c., p. 212)Google Scholar by noting that (ωώ)′ = ώ2, (ωώ2)′ = ώ3, …, (ωώn–1)′ =ώn.
page 238 note * That ∮ω is the only relative integral invariant of the first order for every Hamiltonian system was believed to be true and posed to me by Professor J. S. Wang, to whom I am indebted.
page 238 note † , Whittaker, l.c., p. 269.Google Scholar
page 242 note * , Goursat, l.c., p. 212.Google Scholar
page 242 note † Cartan, E., Lemons sur les invariants intégraux, p. 73.Google Scholar Also , Goursat, l.c., p. 105Google Scholar.
page 242 note ‡ Compare , Whittaker, l.c., § 116.Google Scholar
page 242 note § Where Xi=–Pi, Xn+i=Qi.
page 244 note * A different method (without using integral invariants) of obtaining this condition, in the equivalent form (11.3), and of deducing the equations (11.5) and (11.6), is indicated in Lee, H. C., “Sur les transformations des congruences hamiltoniennes,” Comptes rendus (Paris), CCVI (1938), p. 1431.Google Scholar A generalisation of the method is given in Lee, H. C., “On even-dimensional skew-metric spaces and their groups of transformations,” Amer.Journ. of Math., LXVII (1945), p. 327Google Scholar.
page 244 note † We haye tacitly supposed for generality that the canonical transformation involves the time t. If in particular the new variables ![]() as functions of the old x's are independent of t, (11.6) reduces to
as functions of the old x's are independent of t, (11.6) reduces to ![]() whence ø is a constant (or a function of t). Since to a Hamiltonian function can be added an arbitrary function of t without affecting the corresponding Hamiltonian system, the transformation law (11.5) in this case'may simply be taken in the form
whence ø is a constant (or a function of t). Since to a Hamiltonian function can be added an arbitrary function of t without affecting the corresponding Hamiltonian system, the transformation law (11.5) in this case'may simply be taken in the form ![]() .
.
page 245 note * Many authors, using other methods, come to this conclusion with c – 1 only. See notably Encykl. der Math. Wiss., III, 3, p. 454; Handbuch der Physik, Band V, p. 99; Forsyth, Theory of Differential Equations, part IV, vol. V, p. 399. Although the distinction between c = I and c±I is slight and is not very important in application, it is a difference in theory.
page 246 note * For the conditions of a contact transformation in terms of Lagrange's and Poisson's bracket-expressions, see, e.g., , Whittaker, l.c., pp. 298–300Google Scholar.
page 246 note † That the totality of canonical transformations forms a group can be seen from any one of the conditions (11.2), (11.3), (11.4), (11.7). and (11.10).
page 246 note ‡ Compare, for the special case of a contact transformation, , Whittaker, l.c., p. 295Google Scholar.
page 246 note § , Whittaker, l.c., p. 309.Google Scholar