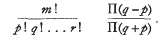Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T01:19:37.695Z Has data issue: false hasContentIssue false
  • English
  • Français

XVI.—On Certain Numerical Coefficients Associated with Partitions

Published online by Cambridge University Press:  14 February 2012

D. E. Rutherford
Get access Rights & Permissions [Opens in a new window]

Extract

§ 1. The principal object of this note is to establish formula (16) of the preceding paper by H. Jack (1966). This formula, which was conjectured by Jack, evaluates a certain coefficient which is attached to a symbol {p, q, …, r}. In this symbols, p, q, …, r form a partition of m such that o≤p≤q≤…≤r,p+q+…+r=m. The symbol however vanishes if any two of the integers p, q, … r are equal but non-zero. In the remaining cases we have to show that the coefficient in question has the value

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 67 , Issue 3 , 1967 , pp. 215 - 219
Copyright
Copyright © Royal Society of Edinburgh 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

Jack, H., 1966. “A Matrix Analogue of the Integral ”, Proc. Roy. Soc. Edin., A, 67, 205–214.Google Scholar
Rutherford, D. E., 1942. “On the Relations between the Numbers of Standard Tableaux”, Proc. Edin. Math. Soc., 7, 51–54.Google Scholar