Published online by Cambridge University Press: 14 February 2012
The problem discussed is that of determining the sequence {an} such that
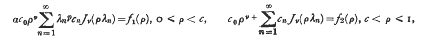
where (λn) is the sequence of positive zeros of the function λJν(λ) + HJν(λ), arranged in order of increasing magnitude, þ, ν and H are real constants (−I <þ < I, ν > −½) and f1(ρ), f2(ρ) are prescribed. By expressing the sequence {cn} in terms of a sequence of integrals involving a function g(t) the problem is reduced to the solution of a non-singular Fredholm integral of the second kind for g(t).