Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-12-01T01:49:38.100Z Has data issue: false hasContentIssue false
  • English
  • Français

XIX.—Asymptotic enumeration of connected graphs

Published online by Cambridge University Press:  14 February 2012

E. M. Wright
E. M. Wright
Affiliation:
University of Aberdeen.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The number of different connected graphs (with some property P) on n labelled nodes with q edges is fnq. Again Fnq is the number of graphs on n labelled nodes with q edges, each of whose connected components has property P. We consider 8 types of graph for which 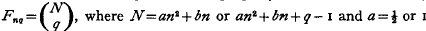. We use a known relation between the generating functions of fnq and Fnq to find an asymptotic expansion of fnq in terms of binomial coefficients, valid if (q – ½n log n)/n→∞ as n→∞. This condition is also necessary for the existence of an asymptotic expansion of this kind.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 68 , Issue 4 , 1970 , pp. 298 - 308
Copyright
Copyright © Royal Society of Edinburgh 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

Erdös, P., and Rényi, A., 1959. “On random graphs I”, Publicationes Math., Debrecen, 6, 290–297.CrossRefGoogle Scholar
Erdös, P., 1960. “On the evolution of random graphs”, Magy. Tudom. Akad. Mat. Kut. Intéz. Közi., 5, 17–61.Google Scholar
Gilbert, E. N., 1956. “Enumeration of labelled graphs”, Can. J. Math., 8, 405–411.CrossRefGoogle Scholar