No CrossRef data available.
Article contents
XII.—On the Theory of Unimolecular Gas Reactions: A Quantum Harmonic Oscillator Model
Published online by Cambridge University Press: 14 February 2012
Synopsis
The writer's theory of unimolecular dissociation rates, based on the treatment of the molecule as a harmonically vibrating system, is put in a form which covers quantum as well as classical mechanics. The classical rate formulæ are as before, and are also the high-temperature limits of the new quantum formulæ. The high-pressure first-order rate k∞ is found first from the Gaussian distribution of co-ordinates and momenta of harmonic systems, and is justified for the quantum-mechanical case by Bartlett and Moyal's phase-space distributions. This leads to a re-formulation of k∞ as a molecular dissociation probability averaged over a continuum of states, and to a general rate for any pressure of the gas.
The high-pressure rate k∞ is of the form ve-F/kT, where v and F depend, in the quantum case, on the temperature T; but v is always between the highest and lowest fundamental vibration frequencies of the molecule. Concerning the decline of the general rate k with pressure 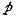 at fixed temperature, k/k∞ is to a certain approximation the same function of
at fixed temperature, k/k∞ is to a certain approximation the same function of 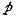 as was tabulated earlier for the classical case, apart from a constant factor changing the pressure scale in the quantum case.
as was tabulated earlier for the classical case, apart from a constant factor changing the pressure scale in the quantum case.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 64 , Issue 2 , 1954 , pp. 161 - 174
- Copyright
- Copyright © Royal Society of Edinburgh 1954


