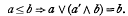Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T02:35:19.619Z Has data issue: false hasContentIssue false
  • English
  • Français

X.—Determinants for Matrices over Lattices

Published online by Cambridge University Press:  14 February 2012

D. S. Chesley  and
J. H. Bevis
D. S. Chesley
Affiliation:
Department of Mathematics, Virginia Polytechnic Institute, Blacksburg, Virginia, U.S.A.
J. H. Bevis
Affiliation:
Department of Mathematics, Virginia Polytechnic Institute, Blacksburg, Virginia, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

In the literature concerning matrices whose co-ordinates are elements of a Boolean lattice, one may find three different definitions for the determinant of a matrix. We shall call these the first, second and third determinant and will denote the value of the ith determinant of a matrix A by |A |i for i = 1, 2, 3. The first determinant may be defined for square matrices over an arbitrary lattice. The second and third determinants may be defined for square matrices over any lattice L with a greatest element I, a least element o and an orthocomplementation′: L→L, that is a′ is a complement of a, a = a″ and a ≤ b implies that b′ ≤ a′ for all a, b in L. In this paper we obtain some elementary properties of these determinants in this general setting and in the particular case where L is an orthomodular lattice, that is a lattice with o, 1 and an orthocomplementation' such that

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 68 , Issue 2 , 1969 , pp. 138 - 144
Copyright
Copyright © Royal Society of Edinburgh 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

[1]Bevis, J. H., 1969. “Matrices over orthomodular lattices”, Glasg. Math. J. [In press].CrossRefGoogle Scholar
[2]Foulis, D. J., 1962. “A note on orthomodular lattices”, Port. Math., 2, 65–72.Google Scholar
[3]Rutherford, D. E., 1963. “Inverses of Boolean Matrices”, Proc. Glasg. Math. Ass., 6, 49–53.CrossRefGoogle Scholar
[4]Sokolov, O. B., 1962. “The application of Boolean determinants to the analysis of logical multiples”, Kazan St. Univ. Sci. Surv. Conf., 109–111.Google Scholar
[5]Wedderburn, J. H. M., 1934. “Boolean linear associative algebra”, Ann. Math., 35, 185–194.CrossRefGoogle Scholar