No CrossRef data available.
Article contents
Well-posedness for strongly damped abstract Cauchy problems of fractional order
Part of:
Groups and semigroups of linear operators, their generalizations and applications
Miscellaneous topics - Partial differential equations
Published online by Cambridge University Press: 13 January 2025
Abstract
Let X be a complex Banach space and B be a closed linear operator with domain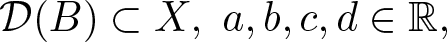 
$\mathcal{D}(B) \subset X,\,\, a,b,c,d\in\mathbb{R},$ and 
$0 \lt \beta \lt \alpha.$ We prove that the problem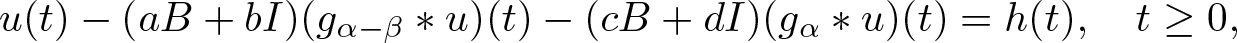
\begin{equation*}u(t) -(aB+bI)(g_{\alpha-\beta}\ast u)(t) -(cB+dI)(g_{\alpha}\ast u)(t) = h(t), \quad t\geq 0,\end{equation*}
where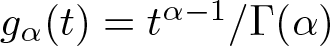 
$g_{\alpha}(t)=t^{\alpha-1}/\Gamma(\alpha)$ and 
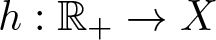$h:\mathbb{R}_+\to X$ is given, has a unique solution for any initial condition on 
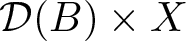$\mathcal{D}(B)\times X$ as long as the operator B generates an ad-hoc Laplace transformable and strongly continuous solution family 
$\{R_{\alpha,\beta}(t)\}_{t\geq 0} \subset \mathcal{L}(X).$ It is shown that such a solution family exists whenever the pair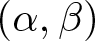 
$(\alpha,\beta)$ belongs to a subset of the set 
$(1,2]\times(0,1]$ and B is the generator of a cosine family or a C0-semigroup in 
$X.$ In any case, it also depends on certain compatibility conditions on the real parameters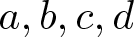 
$a,b,c,d$ that must be satisfied.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Abadias, L. and Miana, P. J.. A subordination principle on Wright functions and regularized resolvent families. J. Funct. Spaces 9 (2015), .Google Scholar
Agarwal, R. P., Jleli, M. and Samet, B.. Nonexistence of global solutions for a time-fractional damped wave equation in a k-times halved space. Comp. & Math. Appl. 78 (2019), 1608–1620.CrossRefGoogle Scholar
Alvarez, E. and Lizama, C.. The super-diffusive singular perturbation problem. Mathematics 8 (2020), 1–14.CrossRefGoogle Scholar
Arendt, W., Batty, C. J. K., Hieber, M. and Neubrander, F.. Vector-valued Laplace transforms and Cauchy problems, Monographs in Mathematics, 2nd edition, 96 (Birkhäuser/Springer Basel AG, Basel, 2011).CrossRefGoogle Scholar
Aviles, P. and Sandefur, J.. Nonlinear second order equations with applications to partial differential equations. J. Diff. Equ. 58 (1985), 404–427.CrossRefGoogle Scholar
Avrin, J. D.. Convergence of the strongly damped nonlinear Klein-Gordon equation in 
$\mathbb{R}^d$ with radial symmetry. Proc. Roy. Soc. Edinburgh Sect. A 107 (1987), 169–174.CrossRefGoogle Scholar
$\mathbb{R}^d$ with radial symmetry. Proc. Roy. Soc. Edinburgh Sect. A 107 (1987), 169–174.CrossRefGoogle ScholarAvrin, J. D.. Convergence properties of the strongly damped nonlinear Klein-Gordon equation. J. Diff. Equ. 67 (1987), 243–255.CrossRefGoogle Scholar
Bateman, H. and Erdélyi, A.. Higher transcendental functions (McGraw-Hill, New York, 1955).Google Scholar
Bazhlekova, E.. Subordination principle for fractional evolution equations. Fract. Calc. Appl. Anal. 3 (2000), 213–230.Google Scholar
Carvalho, A. N., Cholewa, J. W. and Dlotko, T.. Strongly damped wave equations: Bootstrapping and regularity of solutions. J. Diff. Equ. 244 (2008), 2310–2333.CrossRefGoogle Scholar
Dekkers, A. and Rozanova-Pierrat, A.. Cauchy problem for the Kuznetsov equation. Discret. Cont. Dyn. Syst. 39 (2019), 277–307.CrossRefGoogle Scholar
Ding, P. and Yang, Z.. Complete regularity and strong attractor for the strongly damped wave equation with critical nonlinearities on
$\mathbb{R}^3.$ J. Evol. Equ. 23 (2023), .CrossRefGoogle Scholar
$\mathbb{R}^3.$ J. Evol. Equ. 23 (2023), .CrossRefGoogle ScholarGorenflo, G., Kilbas, A. A. and Mainardi, F.. Mittag-Leffler functions, related topics and applications, Monographs in Mathematics, Vol. 2 (Springer, Berlin, 2020).Google Scholar
Ikehata, R., Todorova, G. and Yordanov, B.. Wave equations with strong damping in Hilbert spaces. J. Diff. Equ. 254 (2013), 3352–3368.CrossRefGoogle Scholar
Kaltenbacher, B., Lasiecka, I. and Marchand, R.. Well-posedness and exponential decay rates for the Moore–Gibson–Thompson equation arising in high intensity ultrasound. Control Cybern. 40 (2011), 971–988.Google Scholar
Keyantuo, V. and Lizama, C.. Mild well-posedness of abstract differential equations, Functional Analysis and Evolution Equations (editors Amann, H., Arendt, W., Hieber, M., Neubrander, F. M., Nicaise, S., von Below, J.), (Birkhäuser Verlag, Basel, 2008), 371–387.Google Scholar
Keyantuo, V., Lizama, C. and Poblete, V.. Periodic solutions of integro-differential equations in vector-valued function spaces. J. Diff. Equ. 246 (2009), 1007–1037.CrossRefGoogle Scholar
Keyantuo, V., Lizama, C. and Warma, M.. Asymptotic behavior of fractional order semilinear evolution equations. Diff. Integral Equ. 26 (2013), 757–780.Google Scholar
Keyantuo, V. and Warma, M.. The wave equation with Wentzell-Robin boundary conditions on Lp-spaces. J. Diff. Equ. 229 (2006), 680–697.CrossRefGoogle Scholar
Kirane, M. and Tatar, N. E.. Exponential growth for a fractionally damped wave equation. Z. Anal. Anwend. 22 (2003), 167–177.CrossRefGoogle Scholar
Kostic, M.. (a, k)-regularized C-resolvent families: Regularity and local properties. Abstr. Appl. Anal. 2009 (2009), .CrossRefGoogle Scholar
Kuznetsov, V.. Equations of nonlinear acoustics. Soviet Phys. Acoust. 16 (1971), 467–470.Google Scholar
Lizama, C.. Abstract linear fractional evolution equations, Handbook of Fractional Calculus With Applications. Vol. 2: Fractional Differential Equations (Ed. Kochubei, A. Luchko, Y.), (De Gruyter, Berlin, 2019).Google Scholar
Lizama, C.. Regularized solutions for abstract Volterra equations. J. Math. Anal. Appl. 243 (2000), 278–292.CrossRefGoogle Scholar
Lizama, C. and N’Guérékata, G. M.. Mild solutions for abstract fractional differential equations. Appl. Anal. 92 (2013), 1731–1754.CrossRefGoogle Scholar
Lizama, C. and Prado, H.. Fractional relaxation equations on Banach spaces. Appl. Math. Lett. 23 (2010), 137–142.CrossRefGoogle Scholar
Melnikova, I. V. and Filinkov, A.I.. Well-posedness of differential-operator problems II: The Cauchy problem for complete second-order equations in Banach spaces. J. Math. Sci. 93 (1999), 22–41.CrossRefGoogle Scholar
Neubrander, F.. Well-posedness of higher order abstract Cauchy problems. Trans. Amer. Math. Soc. 295 (1986), 257–290.CrossRefGoogle Scholar
Pang, Y. and Yang, Y.. A note on finite time blowup for dissipative Klein-Gordon equation. Nonlinear Anal. 195 (2020), .CrossRefGoogle Scholar
Podlubny, I.. Fractional differential equations, Mathematics in Science and Engineering 198 (Academic Press, San Diego, 1999).Google Scholar
Prüss, J.. Evolutionary integral equations and applications, Monographs in Mathematics 87 (Birkhäuser, Switzerland, 1993).CrossRefGoogle Scholar
Sandefur, J. T.. Existence and uniqueness of solutions of second order nonlinear differential equations. SIAM J. Math. Anal. 14 (1983), 477–487.CrossRefGoogle Scholar
Stojanovic, M. and Gorenflo, R.. Nonlinear two-term time fractional diffusion-wave problem. Nonlinear Anal. Real World Appl. 11 (2010), 3512–3523.CrossRefGoogle Scholar
Tijun, X. and Jin, L.. On complete second order linear differential equations in Banach spaces. Pacific J. Math. 142 (1990), 175–195.Google Scholar
Titchmarsh, E. C.. The zeros of certain integral functions. Proc. London Math. Soc. 2 (1925), 283–302.Google Scholar
Zhou, Y. and He, J. W.. Well-posedness and regularity for fractional damped wave equations. Monatshefte für Mathematik. 194 (2021), 425–458.CrossRefGoogle Scholar