Published online by Cambridge University Press: 12 July 2007
Let 0 < α ≤ 1 and let M+α be the Cesàro maximal operator of order α defined by
 In this work we characterize the pairs of measurable, positive and locally integrable functions (u, v) for which there exists a constant C > 0 such that the inequality
In this work we characterize the pairs of measurable, positive and locally integrable functions (u, v) for which there exists a constant C > 0 such that the inequality
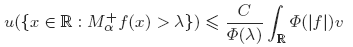 holds for all λ > 0 and every f in the Orlicz space LΦ(v).
We also characterize the measurable, positive and locally integrable functions w such that the integral inequality
holds for all λ > 0 and every f in the Orlicz space LΦ(v).
We also characterize the measurable, positive and locally integrable functions w such that the integral inequality
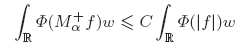 holds for every f ∈ LΦ(w).
The discrete versions of this results allow us, by techniques of transference, to prove weighted inequalities for the Cesàro maximal ergodic operator
holds for every f ∈ LΦ(w).
The discrete versions of this results allow us, by techniques of transference, to prove weighted inequalities for the Cesàro maximal ergodic operator
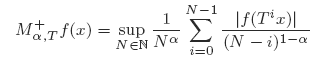 associated with an invertible measurable transformation, T, which preserves the measure.
associated with an invertible measurable transformation, T, which preserves the measure.
Finally, we give sufficient conditions on w for the convergence of the sequence of Cesàro-α ergodic averages for all functions in the weighted Orlicz space LΦ(w).