Let Ω be a bounded Lipschitz domain in R2, let H be a 2 × 2 diagonal matrix with det(H) = 1. Let ε > 0 and consider the functional 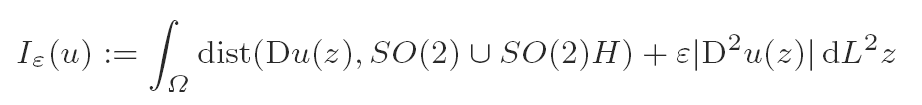over AF ∩ W2,1(Ω), where AF is the class of functions from Ω satisfying affine boundary condition F. It can be shown by convex integration that there exists F ∉ SO(2) ∪ SO(2)H and u ∈ AF with I0(u) = 0. Let 0 < ζ1 < 1 < ζ2 < ∞, .

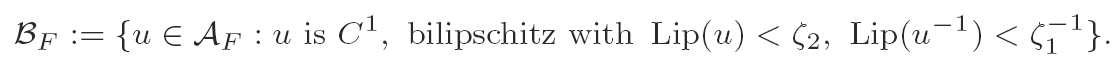In this paper we begin the study of the asymptotics of mε ≔ infBF∩W2,1Iε for such F. This is one of the simplest minimization problems involving surface energy for which we can hope to see the effects of convex integration solutions. The only known lower bounds are lim infε→0mε/ε = ∞.

We link the behaviour of mε to the minimum of I0 over a suitable class of piecewise affine functions. Let {τi} be a triangulation of Ω by triangles of diameter less than h and let 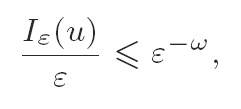denote the class of continuous functions that are piecewise affine on a triangulation {τi}. For the function u ∈ BF let be the interpolant, i.e. the function we obtain by defining ũ⌊τi to be the affine interpolation of u on the corners of τi. We show that if for some small ω > 0 there exists u ∈ BF ∩ W2,1 with then, for h = ε(1+6399ω)/3201, the interpolant satisfies I0(ũ) ≤ h1−cω.

Note that it is trivial that , so we reduce the problem of non-trivial (scaling) lower bounds on mε/ε to the problem of non-trivial lower bounds on .