Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-07-01T02:25:42.877Z Has data issue: false hasContentIssue false
  • English
  • Français

A two point boundary value problem for neutral functional differential equations

Published online by Cambridge University Press:  14 November 2011

Y. G. Sficas  and
S. K. Ntouyas
Y. G. Sficas
Affiliation:
Department of Mathematics, University of Ioannina, Ioannina, Greece
S. K. Ntouyas
Affiliation:
Department of Mathematics, University of Ioannina, Ioannina, Greece
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper is concerned with the existence of solutions of a two point boundary value problem for neutral functional differential equations. We consider the problem

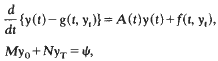
where M and N are n × n matrices. This is examined by using the “shooting method”. Also, an example is given to illustrate how our result can be applied to yield the existence of solutions of a periodic boundary value problem.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 94 , Issue 3-4 , 1983 , pp. 331 - 338
Copyright
Copyright © Royal Society of Edinburgh 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Granas, A.. The theory of compact vector fields and some of its applications to topology and functional spaces I. Rozprawy Math. 30 (1962), 3–91.Google Scholar
2Hale, J. and Cruz, M.. Existence, uniqueness and continuous dependence for hereditary systems. Ann. Mat. Pura Appl 85 (1970), 63–82.CrossRefGoogle Scholar
3Hale, J.. Theory of functional differential equations. Appl. Math. Sci. Vol. 3 (New York: Springer, 1977).CrossRefGoogle Scholar
4Nashed, M. and Wong, J.. Some variants of a fixed point theorem of Rrasnoselskii and applicationsto nonlinear integral equations. J. Math. Mech. 18 (1969), 767–777.Google Scholar
5Sficas, Y. and Ntouyas, S. K.. A boundary value problem for functional differential equations of neutral type. Math. Nachr. (in press).Google Scholar
6Waltman, P. and Wong, J.. Two point boundary value problems for nonlinear functional differentialequations. Trans. Amer. Math. Soc. 164 (1972), 39–54.CrossRefGoogle Scholar