Published online by Cambridge University Press: 10 April 2018
We investigate the structure of the twisted Brauer monoid 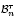 , comparing and contrasting it with the structure of the (untwisted) Brauer monoid
, comparing and contrasting it with the structure of the (untwisted) Brauer monoid 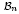 . We characterize Green's relations and pre-orders on
. We characterize Green's relations and pre-orders on 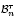 , describe the lattice of ideals and give necessary and sufficient conditions for an ideal to be idempotent generated. We obtain formulae for the rank (smallest size of a generating set) and (where applicable) the idempotent rank (smallest size of an idempotent generating set) of each principal ideal; in particular, when an ideal is idempotent generated, its rank and idempotent rank are equal. As an application of our results, we describe the idempotent generated subsemigroup of
, describe the lattice of ideals and give necessary and sufficient conditions for an ideal to be idempotent generated. We obtain formulae for the rank (smallest size of a generating set) and (where applicable) the idempotent rank (smallest size of an idempotent generating set) of each principal ideal; in particular, when an ideal is idempotent generated, its rank and idempotent rank are equal. As an application of our results, we describe the idempotent generated subsemigroup of 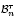 (which is not an ideal), as well as the singular ideal of
(which is not an ideal), as well as the singular ideal of 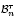 (which is neither principal nor idempotent generated), and we deduce that the singular part of the Brauer monoid
(which is neither principal nor idempotent generated), and we deduce that the singular part of the Brauer monoid 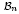 is idempotent generated, a result previously proved by Maltcev and Mazorchuk.
is idempotent generated, a result previously proved by Maltcev and Mazorchuk.