Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T01:42:34.129Z Has data issue: false hasContentIssue false
  • English
  • Français

Trend to spatial homogeneity for solutions to semilinear damped wave equations

Published online by Cambridge University Press:  14 November 2011

J. Solà-Morales  and
M. València
J. Solà-Morales
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, Bellaterra (Barcelona), Spain
M. València
Affiliation:
Departament de Matemàtiques, ETSEIB, Universitat Politècnica de Catalunya, Diagonal 647, 08028 Barcelona, Spain
Get access Rights & Permissions [Opens in a new window]

Synopsis

The semilinear damped wave equations

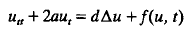
subject to homogeneous Neumann boundary conditions, admit spatially homogeneous solutions (i.e. u(x, t) = u(t)). In order that every solution tends to a spatially homogeneous one, we look for conditions on the coefficients a and d, and on the Lipschitz constant of f with respect to u.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 105 , Issue 1 , 1987 , pp. 117 - 126
Copyright
Copyright © Royal Society of Edinburgh 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Babin, A. V. and Vishik, M. I.. Regular attractors of semigroups and evolution equations. J. Math. Pures Appl. 62 (1983), 441–491.Google Scholar
2Conway, E., Hoff, D. and Smoller, J.. Large time behavior of solutions of systems of nonlinear reaction-diffusion equations. SIAM J. Appl. Math. 35 (1978), 1–16.CrossRefGoogle Scholar
3Hale, J. K.. Asymptotic behavior and dynamics in infinite dimensions. Lefschetz Center of Dynamical Systems, Report 84–28, August, 1984.Google Scholar
4Hale, J. K.. Ordinary differential equations (Malabar: Robert E. Krieger, 1969).Google Scholar
5Othmer, H. G.. Current problems in pattern formation. Lectures Math. Life Sci. 9 (1977), 57–85.Google Scholar
6Segal, I.. Non-linear semigroups. Ann. of Math. 78 (1963), 339–364.CrossRefGoogle Scholar
7Smoller, J.. Shock waves and reaction-diffusion Equations (Berlin: Springer, 1982).Google Scholar
8Stoker, J.. Nonlinear vibrations (New York: Interscience, 1950).Google Scholar