Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T18:47:32.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Travelling wave fronts of Lotka-Volterra reaction-diffusion system in the weak competition case

Part of: Parabolic equations and systems

Published online by Cambridge University Press:  12 August 2021

Yang Wang ,
Hongliang Li  and
Xiong Li
Yang Wang
Affiliation:
School of Mathematical Sciences, Shanxi University, Taiyuan, Shanxi 030006. People's Republic of China ([email protected]) ([email protected])
Hongliang Li
Affiliation:
School of Mathematical Sciences, Shanxi University, Taiyuan, Shanxi 030006. People's Republic of China ([email protected]) ([email protected])
Xiong Li
Affiliation:
Laboratory of Mathematics and Complex Systems (Ministry of Education), School of Mathematical Sciences, Beijing Normal University, Beijing 100875, People's Republic of China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with spreading phenomena of the classical two-species Lotka-Volterra reaction-diffusion system in the weak competition case. More precisely, some new sufficient conditions on the linear or nonlinear speed selection of the minimal wave speed of travelling wave fronts, which connect one half-positive equilibrium and one positive equilibrium, have been given via constructing types of super-sub solutions. Moreover, these conditions for the linear or nonlinear determinacy are quite different from that of the minimal wave speeds of travelling wave fronts connecting other equilibria of Lotka-Volterra competition model. In addition, based on the weighted energy method, we give the global exponential stability of such solutions with large speed 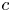$c$. Specially, when the competition rate exerted on one species converges to zero, then for any $c>c_0$, where 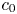$c_0$ is the critical speed, the travelling wave front with the speed 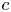$c$ is globally exponentially stable.

Keywords

Lotka-Volterratravelling wave frontsstability

MSC classification

Primary: 35K57: Reaction-diffusion equations
Secondary: 92D25: Population dynamics (general) 92D40: Ecology
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 4 , August 2022 , pp. 912 - 938
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alhasanat, A. and Ou, C.. On a conjecture raised by Yuzo Hosono. J. Dynam. Differ. Equ. 31 (2019), 287–304.CrossRefGoogle Scholar
Alhasanat, A. and Ou, C.. Minimal-speed selection of traveling waves to the Lotka-Volterra competition model. J. Differ. Equ. 266 (2019), 7357–7378.CrossRefGoogle Scholar
Alhasanat, A. and Ou, C.. On the conjecture for the pushed wavefront to the diffusive Lotka-Volterra competition model. J. Math. Biol. 80 (2020), 1413–1422.CrossRefGoogle Scholar
Brown, K. J. and Carr, J.. Deterministic epidemic waves of critical velocity. Math. Proc. Cambridge. Philos. Soc. 81 (1977), 431–433.CrossRefGoogle Scholar
Faye, G. and Holzer, M.. Asymptotic stability of the critical pulled front in a Lotka-Volterra competition model, arXiv:1904.03174.Google Scholar
Girardin, L. and Lam, K. Y.. Invasion of open space by two competitors: spreading properties of monostable two-species competition-diffusion systems. Proc. Lond. Math. Soc. 119 (2019), 1279–1335.CrossRefGoogle Scholar
Hou, X. J. and Leung, A. W.. Traveling wave solutions for a competitive reaction-diffusion system and their asymptotics. Nonlinear Anal. Real. World. Appl. 9 (2008), 2196–2213.CrossRefGoogle Scholar
Lam, K. Y., Salako, R. B. and Wu, Q.. Entire solutions of diffusive Lotka-Volterra system. J. Differ. Equ. 269 (2020), 10758–10791.CrossRefGoogle Scholar
Lewis, M. A., Li, B. T. and Weinberger, H. F.. Spreading speed and linear determinacy for two-species competition models. J. Math. Biol. 45 (2002), 219–233.CrossRefGoogle ScholarPubMed
Li, K., Huang, J. H. and Li, X.. Asymptotic behavior and uniqueness of traveling wave fronts in a delayed nonlocal dispersal competitive system. Commun. Pure. Appl. Anal. 16 (2017), 131–150.CrossRefGoogle Scholar
Li, B. T., Weinberger, H. F. and Lewis, M. A.. Spreading speeds as slowest wave speeds for cooperative systems. Math. Biosci. 196 (2005), 82–98.CrossRefGoogle ScholarPubMed
Liu, Q., Liu, S. and Lam, K. Y.. Asymptotic spreading of interacting species with multiple fronts I: a geometric optics approach, arXiv:1908.05025.Google Scholar
Ma, S.. Traveling wavefronts for delayed reaction-diffusion systems via a fixed point theorem. J. Differ. Equ. 171 (2001), 294–314.CrossRefGoogle Scholar
Ma, M., Chen, D., Yue, J. and Han, Y.. Selection mechanism of the minimal wave speed to the Lotka-Volterra competition model. Appl. Math. Lett. 104 (2020), 106281.CrossRefGoogle Scholar
Mei, M., Lin, C. K., Lin, C. T. and So, J. W. H.. Traveling wavefronts for time-delayed reaction-diffusion equation. I. Local nonlinearity. J. Differ. Equ. 247 (2009), 495–510.CrossRefGoogle Scholar
Mei, M., Ou, C. and Zhao, X. Q.. Global stability of monotone traveling waves for nonlocal time-delayed reaction-diffusion equations. SIAM J. Math. Anal. 42 (2010), 2762–2790.CrossRefGoogle Scholar
Mei, M. and Wang, Y.. Remark on stability of traveling waves for nonlocal Fisher-KPP equations. Int. J. Numer. Anal. Model. Ser. B. 2 (2011), 379–401.Google Scholar
Morita, Y. and Tachibana, K.. An entire solution to the Lotka-Volterra competition-diffusion equations. SIAM J. Math. Anal. 40 (2009), 2217–2240.CrossRefGoogle Scholar
Sattinger, D. H.. On the stability of waves of nonlinear parabolic systems. Advances in Math. 22 (1976), 312–355.CrossRefGoogle Scholar
Sattinger, D. H.. Weighted norms for the stability of traveling waves. J. Differ. Equ. 25 (1977), 130–144.CrossRefGoogle Scholar
Tang, M. M. and Fife, P. C.. Propagating fronts for competing species equations with diffusion. Arch. Rational Mech. Anal. 73 (1980), 69–77.CrossRefGoogle Scholar
Volpert, I., Volpert, V. and Volpert, V.. Traveling wave solutions of parabolic systems. Transl. Math. Monogr., vol. 140 (Providence, RI: American Mathematical Society, 1994).CrossRefGoogle Scholar
Wang, Y. and Li, X.. Entire solutions for the classical competitive Lotka-Volterra system with diffusion in the weak competition case. Nonlinear Anal. Real World Appl. 42 (2018), 1–23.CrossRefGoogle Scholar
Wang, X. H. and Lv, G. Y.. Entire solutions for Lotka-Volterra competition-diffusion model. Int. J. Biomath. 6 (2013), 1350020.CrossRefGoogle Scholar
Wang, Y., Shi, L. L., Liu, G. R. and Ma, Z. H.. The uniqueness and stability of travelling fronts of competitive systems with different diffusive coefficients. IMA J. Appl. Math. 84 (2019), 171–196.CrossRefGoogle Scholar
Yu, Z. X., Xu, F. and Zhang, W. G.. Stability of invasion traveling waves for a competition system with nonlocal dispersals. Appl. Anal. 96 (2017), 1107–1125.CrossRefGoogle Scholar
Yue, Y. X., Han, Y. Z., Tao, J. C. and Ma, M. J.. The minimal wave speed to the Lotka-Volterra competition model. J. Math. Anal. Appl. 488 (2020), 124106430.CrossRefGoogle Scholar
Zhao, X. and Wang, W.. Fisher waves in an epidemic model. Discrete Contin. Dyn. Syst. Ser. B 4 (2004), 1117–1128.Google Scholar
Zhao, X. and Xiao, D.. The asymptotic speed of spread and traveling waves for a vector disease model. J. Dynam. Differ. Equ. 18 (2006), 1001–1019.CrossRefGoogle Scholar