Article contents
Topological regularity of isoperimetric sets in PI spaces having a deformation property
Published online by Cambridge University Press: 09 October 2023
Abstract
We prove topological regularity results for isoperimetric sets in PI spaces having a suitable deformation property, which prescribes a control on the increment of the perimeter of sets under perturbations with balls. More precisely, we prove that isoperimetric sets are open, satisfy boundary density estimates and, under a uniform lower bound on the volumes of unit balls, are bounded. Our results apply, in particular, to the class of possibly collapsed $\mathrm {RCD}(K,N)$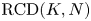 spaces. As a consequence, the rigidity in the isoperimetric inequality on possibly collapsed $\mathrm {RCD}(0,N)$
spaces. As a consequence, the rigidity in the isoperimetric inequality on possibly collapsed $\mathrm {RCD}(0,N)$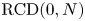 spaces with Euclidean volume growth holds without the additional assumption on the boundedness of isoperimetric sets. Our strategy is of interest even in the Euclidean setting, as it simplifies some classical arguments.
spaces with Euclidean volume growth holds without the additional assumption on the boundedness of isoperimetric sets. Our strategy is of interest even in the Euclidean setting, as it simplifies some classical arguments.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 2
- Cited by



