Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-20T09:34:52.240Z Has data issue: false hasContentIssue false
  • English
  • Français

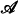A tangent space characterisation of the equivalence of germs for geometric subgroups of and

Published online by Cambridge University Press:  14 November 2011

Ali Lari-Lavassani
Ali Lari-Lavassani
Affiliation:
Centre de Recherches Mathématiques, Université de Montréal, CP 6128-A, Montréal PQ, H3C 3J7, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

It is shown that under the action of a geometric subgroup of and , for a germ f satisfying a certain finiteness condition, given a germ p, if the tangent spaces of f and f + p are equal for all t ∈ [0, 1], then f and f + p are -equivalent.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 125 , Issue 3 , 1995 , pp. 587 - 593
Copyright
Copyright © Royal Society of Edinburgh 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Damon, J.. The Unfolding and Determinacy Theorems for Subgroups of A and K, Mem. Amer. Math. Soc. 306 (Providence, R.I.: American Mathematical Society, 1984).Google Scholar
2Gaffney, T.. Some new results in the classification theory of bifurcation problems. In Multiparameter Bifurcation Theory, Contemporary Mathematics 56 (Providence, R.I.: American Mathematical Society, 1986).CrossRefGoogle Scholar
3Gaffney, T. and Hauser, H.. Characterizing singularities of varieties and of mappings. Inventiones Math. 81 (1985), 427–48.CrossRefGoogle Scholar
4Golubitsky, M. and Langford, W. F.. Classification and unfoldings of degenerate Hopf bifurcations. J. Differential Equations 41 (1981), 375–415.CrossRefGoogle Scholar
5Golubitsky, M. and Marsden, J.. The Morse lemma in infinite dimensions via singularity theory. SIAM J. Math. Anal. 14 (1983), 1037–44.CrossRefGoogle Scholar
6Golubitsky, M. and Schaeffer, D. G.. Imperfect bifurcation in the presence of symmetry. Comm. Math. Phys. 67(1979), 205–32.CrossRefGoogle Scholar
7Golubitsky, M. and Schaeffer, D. G.. Singularities and Groups in Bifurcation Theory, Vol. 1 (New York: Springer, 1985).CrossRefGoogle Scholar
8Golubitsky, M., Stewart, I. and Schaeffer, D. G.. Singularities and Groups in Bifurcation Theory, Vol. 2 (New York: Springer, 1988).CrossRefGoogle Scholar
9Lari-Lavassani, A. and Lu, Y.-C.. Equivariant multiparameter bifurcation via singularity theory. J. Dynamics Differential Equations 5(2) (1993), 189–218.CrossRefGoogle Scholar
10Lari-Lavassani, A. and Lu, Y.-C.. The stability theorems for subgroups of and . Canad. J. Math. 46(1994), 995–1006.CrossRefGoogle Scholar
11Martinet, J.. Singularities of Smooth Functions and Maps, London Mathematical Society Lecture Note Series 58 (Cambridge: Cambridge University Press, 1982).Google Scholar
12Mather, J. and Yau, S. S.. Classification of isolated hypersurface singularities by their moduli algebra. Inventiones Math. 69 (1982), 243–51.CrossRefGoogle Scholar