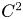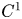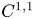1. Introduction
Applications of the theory of optimal transport to Riemannian geometry have had a transformative influence on the field and have led to far-reaching generalizations of classical notions of curvature. In particular, lower Ricci-curvature bounds have been re-cast into convexity conditions on certain entropy functionals, which make sense in settings that go far beyond the original field of Riemannian geometry. Indeed, such curvature (or curvature-dimension) conditions in the sense of Lott–Villani and Sturm can be formulated in general metric measure spaces, where no differentiable structure is available a priori (cf. [Reference Lott and Villani28, Reference Sturm38, Reference Sturm39], as well as the introductory texts [Reference Ambrosio and Gigli2, Reference Villani40]). For Riemannian metrics of regularity $C^2$![]() , these synthetic formulations of lower Ricci curvature bounds are known to be equivalent to the classical (pointwise) estimates ([Reference Cordero-Erausquin, McCann and Schmuckenschläger9, Reference von Renesse and Sturm41], see also [Reference Villani40]).
, these synthetic formulations of lower Ricci curvature bounds are known to be equivalent to the classical (pointwise) estimates ([Reference Cordero-Erausquin, McCann and Schmuckenschläger9, Reference von Renesse and Sturm41], see also [Reference Villani40]).
In particular, synthetic Ricci curvature bounds can be imposed on Riemannian metrics whose regularity lies strictly below $C^2$![]() . On the other hand, for such metrics, there is another, more analytic, way of making sense of curvature bounds, namely by calculating the curvature quantities directly in the space of Schwartz distributions and then imposing distributional inequalities as curvature bounds. Also this approach reduces to the classical pointwise estimates as soon as the regularity of the metric is at least $C^2$
. On the other hand, for such metrics, there is another, more analytic, way of making sense of curvature bounds, namely by calculating the curvature quantities directly in the space of Schwartz distributions and then imposing distributional inequalities as curvature bounds. Also this approach reduces to the classical pointwise estimates as soon as the regularity of the metric is at least $C^2$![]() . Especially in physics, be it in classical electrodynamics, general relativity or quantum field theory, this analytic approach is widely used to model singular sources or fields or to describe matched spacetimes (cf., e.g. [Reference Bär, Ginoux and Pfäffle4, Reference Steinbauer and Vickers37] and references therein). In recent years, distributional Ricci bounds (in the shape of strong energy conditions) have also featured prominently in the generalization of the classical singularity theorems of Penrose and Hawking to spacetime metrics of regularity below $C^2$
. Especially in physics, be it in classical electrodynamics, general relativity or quantum field theory, this analytic approach is widely used to model singular sources or fields or to describe matched spacetimes (cf., e.g. [Reference Bär, Ginoux and Pfäffle4, Reference Steinbauer and Vickers37] and references therein). In recent years, distributional Ricci bounds (in the shape of strong energy conditions) have also featured prominently in the generalization of the classical singularity theorems of Penrose and Hawking to spacetime metrics of regularity below $C^2$![]() ([Reference Graf14, Reference Graf, Grant, Kunzinger and Steinbauer15, Reference Kunzinger, Ohanyan, Schinnerl and Steinbauer20, Reference Kunzinger, Steinbauer, Stojković and Vickers24, Reference Kunzinger, Steinbauer and Vickers25]). On the synthetic side, a generalization of Hawking's singularity theorem to Lorentzian synthetic spaces was established by Cavalletti and Mondino in [Reference Cavalletti and Mondino6].
([Reference Graf14, Reference Graf, Grant, Kunzinger and Steinbauer15, Reference Kunzinger, Ohanyan, Schinnerl and Steinbauer20, Reference Kunzinger, Steinbauer, Stojković and Vickers24, Reference Kunzinger, Steinbauer and Vickers25]). On the synthetic side, a generalization of Hawking's singularity theorem to Lorentzian synthetic spaces was established by Cavalletti and Mondino in [Reference Cavalletti and Mondino6].
A natural question arising in this context is whether the synthetic and the distributional approach to lower Ricci curvature bounds continue to agree for metrics of regularity strictly below $C^2$![]() . We analyse this problem for Riemannian metrics of class $C^1$
. We analyse this problem for Riemannian metrics of class $C^1$![]() and $C^{1,1}$
and $C^{1,1}$![]() on compact manifolds, comparing distributional Ricci bounds with $\infty$
on compact manifolds, comparing distributional Ricci bounds with $\infty$![]() -Ricci bounds in the sense of Lott–Villani ([Reference Lott and Villani28, Reference Sturm38, Reference Sturm39]). Our main results are that, on the one hand, distributional lower Ricci bounds imply lower $\infty$
-Ricci bounds in the sense of Lott–Villani ([Reference Lott and Villani28, Reference Sturm38, Reference Sturm39]). Our main results are that, on the one hand, distributional lower Ricci bounds imply lower $\infty$![]() -Ricci bounds for $C^1$
-Ricci bounds for $C^1$![]() -metrics (theorem 5.4), and that, conversely, lower $\infty$
-metrics (theorem 5.4), and that, conversely, lower $\infty$![]() -Ricci bounds on a $C^{1,1}$
-Ricci bounds on a $C^{1,1}$![]() -Riemannian metric imply the corresponding distributional bounds under an additional convergence condition on regularizations of the metric (theorem 6.4).
-Riemannian metric imply the corresponding distributional bounds under an additional convergence condition on regularizations of the metric (theorem 6.4).
Technically, our approach rests on a characterization of distributional curvature bounds via regularization (theorem 4.3), and on a refined study of properties of the exponential map of a $C^{1,1}$![]() -metric due to Minguzzi ([Reference Minguzzi31]). The latter in particular makes it possible to directly generalize a number of essential properties of optimal transport on Riemannian manifolds (as laid out in McCann's fundamental work [Reference McCann30]) from the regularity class $C^2$
-metric due to Minguzzi ([Reference Minguzzi31]). The latter in particular makes it possible to directly generalize a number of essential properties of optimal transport on Riemannian manifolds (as laid out in McCann's fundamental work [Reference McCann30]) from the regularity class $C^2$![]() to $C^{1,1}$
to $C^{1,1}$![]() . This is the content of § 2. In § 3 we give a brief overview of distributional Riemannian geometry and curvature bounds in this setting. The regularization results we require are derived in § 4. The remaining § 5 and 6 are devoted to proving the main results stated above.
. This is the content of § 2. In § 3 we give a brief overview of distributional Riemannian geometry and curvature bounds in this setting. The regularization results we require are derived in § 4. The remaining § 5 and 6 are devoted to proving the main results stated above.
2. Fundamentals of optimal transport for $C^{1,1}$ -metrics
-metrics
In this section, we closely follow the fundamental paper [Reference McCann30] and show that its results carry over unchanged from Riemannian metrics of regularity $C^2$![]() to those of class $C^{1,1}$
to those of class $C^{1,1}$![]() . Let $M$
. Let $M$![]() be a compact connected Riemannian manifold without boundary. We shall assume $M$
be a compact connected Riemannian manifold without boundary. We shall assume $M$![]() to be $C^\infty$
to be $C^\infty$![]() -smooth, but all results derived below hold for $C^{2,1}$
-smooth, but all results derived below hold for $C^{2,1}$![]() -manifolds as well. Indeed, by [Reference Hirsch19, Th. 2.9], for any $C^k$
-manifolds as well. Indeed, by [Reference Hirsch19, Th. 2.9], for any $C^k$![]() -manifold ($k\ge 1$
-manifold ($k\ge 1$![]() ), there exists a unique $C^k$
), there exists a unique $C^k$![]() -compatible $C^\infty$
-compatible $C^\infty$![]() -atlas on $M$
-atlas on $M$![]() . We are studying the Monge problem for probability measures $\mu,\, \nu$
. We are studying the Monge problem for probability measures $\mu,\, \nu$![]() on $M$
on $M$![]() with cost function $c(x,\,y)=d^2(x,\,y)/2$
with cost function $c(x,\,y)=d^2(x,\,y)/2$![]() , where $d$
, where $d$![]() is the Riemannian distance on $M$
is the Riemannian distance on $M$![]() . Thus, we are looking for a map $S:M\to M$
. Thus, we are looking for a map $S:M\to M$![]() that minimizes the transportation cost
that minimizes the transportation cost
among all Borel maps $S$![]() that push forward $\mu$
that push forward $\mu$![]() to $\nu$
to $\nu$![]() , $S_\# \mu = \nu$
, $S_\# \mu = \nu$![]() , and we call the set of these maps $\mathcal {S}(\mu,\,\nu )$
, and we call the set of these maps $\mathcal {S}(\mu,\,\nu )$![]() . For any $\psi : M\to \mathbb {R}\cup \{\pm \infty \}$
. For any $\psi : M\to \mathbb {R}\cup \{\pm \infty \}$![]() , we define its infimal convolution by
, we define its infimal convolution by
The dual Kantorovich problem consists in finding $(\psi,\,\phi )$![]() maximizing
maximizing
over the set $\mathrm {Lip}_c := \{(u,\,v) \mid u,\,v:M\to \mathbb {R}\ \mathrm {continuous},\, \forall (x,\,y): u(x)+v(y) \le c(x,\,y)\}$![]() .
.
As a preparation for the following results, we collect some general properties of the exponential map and the distance function of a $C^{1,1}$![]() -Riemannian metric. By [Reference Minguzzi31, Th. 4] (or also [Reference Kunzinger, Steinbauer and Stojković22, Th. 4.1]), any $x\in M$
-Riemannian metric. By [Reference Minguzzi31, Th. 4] (or also [Reference Kunzinger, Steinbauer and Stojković22, Th. 4.1]), any $x\in M$![]() possesses a convex normal neighbourhood $U$
possesses a convex normal neighbourhood $U$![]() (called a totally normal neighbourhood in [Reference Kunzinger, Steinbauer and Stojković22]). This means that for any $y\in U$
(called a totally normal neighbourhood in [Reference Kunzinger, Steinbauer and Stojković22]). This means that for any $y\in U$![]() , $U$
, $U$![]() is a normal neighbourhood of $y$
is a normal neighbourhood of $y$![]() , i.e. $\exp _y$
, i.e. $\exp _y$![]() is a bi-Lipschitz homeomorphism from a star-shaped open neighbourhood of $0$
is a bi-Lipschitz homeomorphism from a star-shaped open neighbourhood of $0$![]() in $T_yM$
in $T_yM$![]() onto $U$
onto $U$![]() . In particular, Rademacher's theorem (cf. [Reference McCann30, Lem. 4] for the version we use here) implies that $\exp _y^{-1}$
. In particular, Rademacher's theorem (cf. [Reference McCann30, Lem. 4] for the version we use here) implies that $\exp _y^{-1}$![]() is differentiable almost everywhere on its domain, as is $\exp _y$
is differentiable almost everywhere on its domain, as is $\exp _y$![]() . By [Reference Minguzzi31, Th. 6], the unique shortest absolutely continuous curve $\sigma$
. By [Reference Minguzzi31, Th. 6], the unique shortest absolutely continuous curve $\sigma$![]() in $M$
in $M$![]() from $y\in U$
from $y\in U$![]() to $x$
to $x$![]() is (has a reparametrization as) the radial geodesic $\sigma :[0,\,1]\to M$
is (has a reparametrization as) the radial geodesic $\sigma :[0,\,1]\to M$![]() , $\sigma (t) = \exp _y(t\cdot \exp _y^{-1}x)$
, $\sigma (t) = \exp _y(t\cdot \exp _y^{-1}x)$![]() . In particular, for the Riemannian distance of $x$
. In particular, for the Riemannian distance of $x$![]() and $y$
and $y$![]() , we obtain
, we obtain
Covering a minimizing curve between points that are not necessarily contained in a common convex normal neighbourhood by such neighbourhoods and applying the above, we conclude that also in this case the curve has a reparametrization as an unbroken geodesic, hence in particular of regularity $C^{2,1}$![]() (as follows directly from the geodesic equation).
(as follows directly from the geodesic equation).
Furthermore, for any $x\in M$![]() , $v\mapsto \exp _x v$
, $v\mapsto \exp _x v$![]() is strongly differentiable (in the sense of Peano, cf. [Reference Minguzzi31, Def. 2]) at $v=0$
is strongly differentiable (in the sense of Peano, cf. [Reference Minguzzi31, Def. 2]) at $v=0$![]() with strong differential $T_0\exp _x = \mathrm {id}_{T_xM}$
with strong differential $T_0\exp _x = \mathrm {id}_{T_xM}$![]() ([Reference Minguzzi31, Th. 3 and Sec. 2.3]). By Leach's inverse function theorem (cf. [Reference Minguzzi31, Th. 2]), also $z\mapsto \exp _x^{-1}(z)$
([Reference Minguzzi31, Th. 3 and Sec. 2.3]). By Leach's inverse function theorem (cf. [Reference Minguzzi31, Th. 2]), also $z\mapsto \exp _x^{-1}(z)$![]() is strongly differentiable at $z=x$
is strongly differentiable at $z=x$![]() with strong differential $\mathrm {id}_{T_xM}$
with strong differential $\mathrm {id}_{T_xM}$![]() . In particular, the corresponding statements with standard differentials are valid as well. Also the Gauss lemma holds at every point $x\in U$
. In particular, the corresponding statements with standard differentials are valid as well. Also the Gauss lemma holds at every point $x\in U$![]() where $\exp _y$
where $\exp _y$![]() is differentiable ([Reference Minguzzi31, Th. 5]): for such $x$
is differentiable ([Reference Minguzzi31, Th. 5]): for such $x$![]() , $v_1 := \exp _y^{-1}(x)$
, $v_1 := \exp _y^{-1}(x)$![]() and any $v_2\in T_yM\cong T_{v_1}(T_yM)$
and any $v_2\in T_yM\cong T_{v_1}(T_yM)$![]() we have:
we have:
Finally, it is proved in ([Reference Minguzzi31, Th. 5]) that the map $D_y^2:=x\mapsto g(\exp _y^{-1}x,\,\exp _y^{-1}x)$![]() is of differentiability class $C^{1,1}$
is of differentiability class $C^{1,1}$![]() on $U$
on $U$![]() , with tangent map
, with tangent map
where $\sigma (t)=\exp _y(t\cdot \exp _y^{-1}x)$![]() is as above, and $(y,\,x)\mapsto P(y,\,x):=\dot \sigma (1)$
is as above, and $(y,\,x)\mapsto P(y,\,x):=\dot \sigma (1)$![]() is the position vector field of $x$
is the position vector field of $x$![]() with respect to $y$
with respect to $y$![]() .
.
Based on these results, we can now extend the validity of [Reference McCann30, Prop. 6] to Riemannian metrics $g\in C^{1,1}$![]() :
:
Proposition 2.1 Let $(M,\,g)$![]() be a $C^{1,1}$
be a $C^{1,1}$![]() -Riemannian manifold (with or without boundary). Let $y\in M$
-Riemannian manifold (with or without boundary). Let $y\in M$![]() and set $\phi : M\to \mathbb {R},$
and set $\phi : M\to \mathbb {R},$![]() $\phi (x):= d^2(x,\,y)/2$
$\phi (x):= d^2(x,\,y)/2$![]() . Then:
. Then:
(i) There exists a neighbourhood $U$
 of $y$
of $y$ such that $\phi$
such that $\phi$ is differentiable at every point in $U$
is differentiable at every point in $U$ .
.(ii) For each $x\in M$
 , if there exists a distance-realizing absolutely continuous curve $\sigma$
, if there exists a distance-realizing absolutely continuous curve $\sigma$ from $y$
from $y$ to $x$
to $x$ , then $\sigma$
, then $\sigma$ can be parametrized as a geodesic $\sigma : [0,\,1]\to M$
can be parametrized as a geodesic $\sigma : [0,\,1]\to M$ and $\phi$
and $\phi$ has supergradient $\dot \sigma (1)\in \bar \partial \phi _x$
has supergradient $\dot \sigma (1)\in \bar \partial \phi _x$ at $x$
at $x$ .
.
Proof. (i) Pick a convex normal neighbourhood $U\subseteq M$![]() of $y$
of $y$![]() . Then for any $x\in U$
. Then for any $x\in U$![]() , by (2.3) we have $\phi (x) = \frac {1}{2} D^2_y(x)$
, by (2.3) we have $\phi (x) = \frac {1}{2} D^2_y(x)$![]() , so (2.4) gives $\nabla \phi (x) = \dot \sigma (1)$
, so (2.4) gives $\nabla \phi (x) = \dot \sigma (1)$![]() . Using $d(x,\,y) = \sqrt {2\phi (x)}$
. Using $d(x,\,y) = \sqrt {2\phi (x)}$![]() , we conclude that $\nabla _x d(x,\,y) = \dot \sigma (1)/|\dot \sigma (1)|_x$
, we conclude that $\nabla _x d(x,\,y) = \dot \sigma (1)/|\dot \sigma (1)|_x$![]() for $x\not =y$
for $x\not =y$![]() .
.
(ii) This now follows exactly as in [Reference McCann30, Prop. 6]. For the reader's convenience, we include the argument. Suppose that $y$![]() does not lie in a convex normal neighbourhood $U$
does not lie in a convex normal neighbourhood $U$![]() around $x$
around $x$![]() and let $\sigma$
and let $\sigma$![]() be a minimizing a.c. curve from $y$
be a minimizing a.c. curve from $y$![]() to $x$
to $x$![]() . By what was said above, $\sigma$
. By what was said above, $\sigma$![]() possesses a parametrization as an unbroken geodesic $[0,\,1]\to M$
possesses a parametrization as an unbroken geodesic $[0,\,1]\to M$![]() with $y=\sigma (0)$
with $y=\sigma (0)$![]() and $x=\sigma (1)$
and $x=\sigma (1)$![]() . Pick $z\ne x$
. Pick $z\ne x$![]() on $\sigma$
on $\sigma$![]() such that $z\in U$
such that $z\in U$![]() . Then (i) gives $\nabla _x d(x,\,z) = \dot \sigma (1)/|\dot \sigma (1)|_x$
. Then (i) gives $\nabla _x d(x,\,z) = \dot \sigma (1)/|\dot \sigma (1)|_x$![]() . Since $T_0\exp _x = \mathrm {id}_{T_xM}$
. Since $T_0\exp _x = \mathrm {id}_{T_xM}$![]() , for any $v\in T_xM$
, for any $v\in T_xM$![]() we have
we have
which combined with the triangle inequality and the fact that $z$![]() lies on $\sigma$
lies on $\sigma$![]() leads to
leads to
This shows that $d(y,\,.\,) = \sqrt {2\phi }$![]() is superdifferentiable at $x$
is superdifferentiable at $x$![]() and the chain rule [Reference McCann30, Lem. 5] finally gives $\dot \sigma (1) \in \bar \partial \phi _x$
and the chain rule [Reference McCann30, Lem. 5] finally gives $\dot \sigma (1) \in \bar \partial \phi _x$![]() , as claimed.
, as claimed.
Proposition 2.1 is the key to transferring all further results from [Reference McCann30, Sec. 3] to $C^{1,1}$![]() -metrics. We begin with [Reference McCann30, Lem. 7]:
-metrics. We begin with [Reference McCann30, Lem. 7]:
Lemma 2.2 Let $M$![]() be a connected closed Riemannian manifold with $g\in C^{1,1}$
be a connected closed Riemannian manifold with $g\in C^{1,1}$![]() and let $\psi : M\to \mathbb {R},$
and let $\psi : M\to \mathbb {R},$![]() $\psi =\psi ^{cc}$
$\psi =\psi ^{cc}$![]() . Then $c(x,\,y) -\psi (x) -\psi ^c(y) \ge 0$
. Then $c(x,\,y) -\psi (x) -\psi ^c(y) \ge 0$![]() for all $x,\,y\in M,$
for all $x,\,y\in M,$![]() and if $\psi$
and if $\psi$![]() is differentiable in $x$
is differentiable in $x$![]() then equality holds if and only if $y=\exp _x(-\nabla \psi (x))$
then equality holds if and only if $y=\exp _x(-\nabla \psi (x))$![]() .
.
Proof. This follows exactly as in [Reference McCann30, Lem. 7], only noting that the Hopf–Rinow theorem remains true in this regularity (indeed even for $g\in C^0$![]() , cf. [Reference Burago, Burago and Ivanov5, 2.5.28]) and the fact that minimizers are geodesics, hence $C^{2,1}$
, cf. [Reference Burago, Burago and Ivanov5, 2.5.28]) and the fact that minimizers are geodesics, hence $C^{2,1}$![]() by what was said above.
by what was said above.
Note that any $\psi$![]() as in the previous lemma is Lipschitz continuous, hence differentiable a.e. by [Reference McCann30, Lem. 2]. Based on the above results, the proofs of theorems 8 and 9 in [Reference McCann30] carry over verbatim to the current situation to give:
as in the previous lemma is Lipschitz continuous, hence differentiable a.e. by [Reference McCann30, Lem. 2]. Based on the above results, the proofs of theorems 8 and 9 in [Reference McCann30] carry over verbatim to the current situation to give:
Theorem 2.3 Let $M$![]() be a connected closed manifold with a $C^{1,1}$
be a connected closed manifold with a $C^{1,1}$![]() -Riemannian metric $g$
-Riemannian metric $g$![]() and let $\mu,\, \nu$
and let $\mu,\, \nu$![]() be Borel probability measures on $M$
be Borel probability measures on $M$![]() with $\mu \ll \mathrm {vol_g}$
with $\mu \ll \mathrm {vol_g}$![]() . Also, let $c(x,\,y) = d(x,\,y)^2/2$
. Also, let $c(x,\,y) = d(x,\,y)^2/2$![]() . Then:
. Then:
(i) (Uniqueness) If $\psi : M\to \mathbb {R}$
 satisfies $\psi =\psi ^{cc}$
satisfies $\psi =\psi ^{cc}$ , then $T: x\mapsto \exp _x(-\nabla \psi (x))$
, then $T: x\mapsto \exp _x(-\nabla \psi (x))$ minimizes (2.1) among all Borel maps $S$
minimizes (2.1) among all Borel maps $S$ with $S_\#\mu = T_\# \mu$
with $S_\#\mu = T_\# \mu$ . Any other such map must equal $T$
. Any other such map must equal $T$ $\mu$
$\mu$ -almost everywhere.
-almost everywhere.(ii) (Existence) There exists a potential $\psi : M\to \mathbb {R}$
 with $\psi =\psi ^{cc}$
with $\psi =\psi ^{cc}$ such that $T: x\mapsto \exp _x(-\nabla \psi (x))$
such that $T: x\mapsto \exp _x(-\nabla \psi (x))$ satisfies $T_\# \mu = \nu$
satisfies $T_\# \mu = \nu$ . Any other potential that pushes $\mu$
. Any other potential that pushes $\mu$ forward to $\nu$
forward to $\nu$ gives rise to the same map $T$
gives rise to the same map $T$ , up to a set of $\mu$
, up to a set of $\mu$ -measure $0$
-measure $0$ .
.
By Kantorovich duality ([Reference Villani40, Th. 5.10]), it follows that for $\psi$![]() and $T$
and $T$![]() as in theorem 2.3, we have
as in theorem 2.3, we have

where $\Pi (\mu,\,\nu )$![]() denotes the set of all couplings between $\mu$
denotes the set of all couplings between $\mu$![]() and $\nu$
and $\nu$![]() .
.
We note that also invertibility of $T$![]() ([Reference McCann30, Cor. 10]) and polar factorization of maps ([Reference McCann30, Th. 11]) carry over unchanged to $C^{1,1}$
([Reference McCann30, Cor. 10]) and polar factorization of maps ([Reference McCann30, Th. 11]) carry over unchanged to $C^{1,1}$![]() -metrics.
-metrics.
3. Distributional curvature quantities
In order to lay out the distributional approach to curvature bounds for metrics of low regularity within a consistent framework, we are going to employ the theory of distributional connections due to LeFloch and Mardare ([Reference LeFloch and Mardare27], cf. also [Reference Grosser, Kunzinger, Oberguggenberger and Steinbauer17, Reference Marsden29, Reference Steinbauer36]), which we briefly summarize below.
For $k\in \mathbb {N}_0\cup \{\infty \}$![]() , let $\mathrm {Vol}(M)$
, let $\mathrm {Vol}(M)$![]() denote the volume bundle over $M$
denote the volume bundle over $M$![]() , and $\Gamma ^k_c(M,\,\mathrm {Vol}(M))$
, and $\Gamma ^k_c(M,\,\mathrm {Vol}(M))$![]() the space of compactly supported $C^k$
the space of compactly supported $C^k$![]() one-densities on $M$
one-densities on $M$![]() (i.e. sections of $\mathrm {Vol}(M)$
(i.e. sections of $\mathrm {Vol}(M)$![]() ) that are $k$
) that are $k$![]() times continuously differentiable. Then the space of distributions of order $k$
times continuously differentiable. Then the space of distributions of order $k$![]() on $M$
on $M$![]() is the topological dual of $\Gamma ^k_c(M,\,\mathrm {Vol}(M))$
is the topological dual of $\Gamma ^k_c(M,\,\mathrm {Vol}(M))$![]() (cf. [Reference Grosser, Kunzinger, Oberguggenberger and Steinbauer17, Sec. 3.1]):
(cf. [Reference Grosser, Kunzinger, Oberguggenberger and Steinbauer17, Sec. 3.1]):
For $k=\infty$![]() , we will omit superscript $(k)$
, we will omit superscript $(k)$![]() . There are topological embeddings $\mathcal {D}'{}^{(k)}(M) \hookrightarrow {\mathcal {D}'}{}^{(k+1)}(M) \hookrightarrow \mathcal {D}'(M)$
. There are topological embeddings $\mathcal {D}'{}^{(k)}(M) \hookrightarrow {\mathcal {D}'}{}^{(k+1)}(M) \hookrightarrow \mathcal {D}'(M)$![]() for all $k$
for all $k$![]() . The space of distributional $(r,\,s)$
. The space of distributional $(r,\,s)$![]() -tensor fields of order $k$
-tensor fields of order $k$![]() is defined as
is defined as
Furthermore (cf. [Reference Grosser, Kunzinger, Oberguggenberger and Steinbauer17, 3.1.15]), denoting by $\mathfrak {X}(M)$![]() the space of smooth vector fields on $M$
the space of smooth vector fields on $M$![]() and by $\Omega ^1(M)$
and by $\Omega ^1(M)$![]() that of smooth one-forms,
that of smooth one-forms,
and in fact these isomorphisms hold in the bornological sense ([Reference Nigsch32]). Analogous isomorphisms hold in finite differentiability classes: For the $C^k(M)$![]() -module $\Gamma _{C^k}(M,\,F)$
-module $\Gamma _{C^k}(M,\,F)$![]() ($1\le k \le \infty$
($1\le k \le \infty$![]() ), we have:
), we have:

The space of smooth tensor fields is continuously and densely embedded via

where $\omega$![]() is a one-density. We note that the dense embedding of $\mathcal {T}^r_s(M)$
is a one-density. We note that the dense embedding of $\mathcal {T}^r_s(M)$![]() in $\mathcal {D}'{}^{(k)}\mathcal {T}^r_s(M)$
in $\mathcal {D}'{}^{(k)}\mathcal {T}^r_s(M)$![]() already fixes the form of all the operations on distributional tensor fields to be introduced below since we want to have compatibility with smooth Riemannian geometry.
already fixes the form of all the operations on distributional tensor fields to be introduced below since we want to have compatibility with smooth Riemannian geometry.
Any $t\in \mathcal {T}^r_s(M)$![]() possesses a unique extension to a map that acts on distributions in one of its arguments: if $\tilde \theta _1 \in \mathcal {D}'\mathcal {T}^0_1(M)$
possesses a unique extension to a map that acts on distributions in one of its arguments: if $\tilde \theta _1 \in \mathcal {D}'\mathcal {T}^0_1(M)$![]() , then since $t(\,.\,,\,\theta _2,\,\dots,\,X_s)\in \mathfrak {X}(M)$
, then since $t(\,.\,,\,\theta _2,\,\dots,\,X_s)\in \mathfrak {X}(M)$![]() , we may set
, we may set
and analogously for the other arguments.
Definition 3.1 A distributional connection is a map
such that for $X,\,X',\,Y,\,Y'\in \mathfrak {X}(M)$![]() and $f\in C^\infty (M)$
and $f\in C^\infty (M)$![]() the usual computational rules hold: $\nabla _{f X+X'}Y = f\nabla _XY + \nabla _{X'}Y$
the usual computational rules hold: $\nabla _{f X+X'}Y = f\nabla _XY + \nabla _{X'}Y$![]() , $\nabla _X(Y+Y') = \nabla _X Y +\nabla _X Y'$
, $\nabla _X(Y+Y') = \nabla _X Y +\nabla _X Y'$![]() , $\nabla _X(f Y) = X(f)Y + f\nabla _X Y$
, $\nabla _X(f Y) = X(f)Y + f\nabla _X Y$![]() . It is called an $L^2_{\mathrm {loc}}$
. It is called an $L^2_{\mathrm {loc}}$![]() -connection, $\nabla \in L^2_{\mathrm {loc}}$
-connection, $\nabla \in L^2_{\mathrm {loc}}$![]() , if $\nabla _X Y$
, if $\nabla _X Y$![]() is an $L^2_{\mathrm {loc}}$
is an $L^2_{\mathrm {loc}}$![]() -vector field for any $X,\,Y\in \mathfrak {X}(M)$
-vector field for any $X,\,Y\in \mathfrak {X}(M)$![]() (cf. [Reference LeFloch and Mardare27, Sec. 3]).
(cf. [Reference LeFloch and Mardare27, Sec. 3]).
More generally, denoting by ${\mathcal {G}}$![]() any of the spaces $C^k$
any of the spaces $C^k$![]() $(0\leq k)$
$(0\leq k)$![]() or $L^p_{\mathrm {loc}}$
or $L^p_{\mathrm {loc}}$![]() $(1\leq p)$
$(1\leq p)$![]() , we call a distributional connection a ${\mathcal {G}}$
, we call a distributional connection a ${\mathcal {G}}$![]() -connection if $\nabla _X Y$
-connection if $\nabla _X Y$![]() is a ${\mathcal {G}}$
is a ${\mathcal {G}}$![]() -vector field for any $X,\,Y\in \mathfrak {X}(M)$
-vector field for any $X,\,Y\in \mathfrak {X}(M)$![]() . $L^2_{\mathrm {loc}}$
. $L^2_{\mathrm {loc}}$![]() -connections play a distinguished role in this hierarchy since they form the largest class for which there is a stable definition of the curvature tensor in distributions, cf. [Reference Geroch and Traschen12, Reference LeFloch and Mardare27, Reference Steinbauer36].
-connections play a distinguished role in this hierarchy since they form the largest class for which there is a stable definition of the curvature tensor in distributions, cf. [Reference Geroch and Traschen12, Reference LeFloch and Mardare27, Reference Steinbauer36].
Any $L^2_{\mathrm {loc}}$![]() -connection can be extended to a map $\nabla : \mathfrak {X}(M) \times \mathfrak {X}_{L^2_{\mathrm {loc}}}(M) \to \mathcal {D}' \mathcal {T}^1_0(M)$
-connection can be extended to a map $\nabla : \mathfrak {X}(M) \times \mathfrak {X}_{L^2_{\mathrm {loc}}}(M) \to \mathcal {D}' \mathcal {T}^1_0(M)$![]() by setting
by setting
Based on this extension, we can assign a Riemann tensor to each $L^2_{\mathrm {loc}}$![]() -connection as follows ([Reference LeFloch and Mardare27, Def. 3.3]):
-connection as follows ([Reference LeFloch and Mardare27, Def. 3.3]):
Definition 3.2 The distributional Riemann tensor of an $L^2_{\mathrm {loc}}$![]() -connection $\nabla$
-connection $\nabla$![]() is the map $R: \mathfrak {X}(M)^3 \to \mathcal {D}'\mathcal {T}^1_0(M)$
is the map $R: \mathfrak {X}(M)^3 \to \mathcal {D}'\mathcal {T}^1_0(M)$![]() ,
,
for $X,\,Y,\,Z\in \mathfrak {X}(M)$![]() and $\theta \in \Omega ^1(M)$
and $\theta \in \Omega ^1(M)$![]() ,
,
If $F_i$![]() is a smooth local frame in $\mathfrak {X}(U)$
is a smooth local frame in $\mathfrak {X}(U)$![]() and $F^j\in \Omega ^1(U)$
and $F^j\in \Omega ^1(U)$![]() its dual frame (i.e. ${F^j(F_i) = \delta _{i}^j}$
its dual frame (i.e. ${F^j(F_i) = \delta _{i}^j}$![]() ), then the Ricci tensor corresponding to $\nabla$
), then the Ricci tensor corresponding to $\nabla$![]() is given by (using the Einstein summation convention)
is given by (using the Einstein summation convention)
and is readily seen not to depend on the choice of local frame.
A distributional Riemannian metric on $M$![]() ([Reference Grosser, Kunzinger, Oberguggenberger and Steinbauer17, Reference LeFloch and Mardare27, Reference Marsden29]) is an element of $\mathcal {D}'\mathcal {T}^0_2(M)$
([Reference Grosser, Kunzinger, Oberguggenberger and Steinbauer17, Reference LeFloch and Mardare27, Reference Marsden29]) is an element of $\mathcal {D}'\mathcal {T}^0_2(M)$![]() that is symmetric and non-degenerate in the sense that $g(X,\,Y)=0$
that is symmetric and non-degenerate in the sense that $g(X,\,Y)=0$![]() for all $Y\in \mathfrak {X}(M)$
for all $Y\in \mathfrak {X}(M)$![]() implies $X=0$
implies $X=0$![]() . In particular, any $C^1$
. In particular, any $C^1$![]() -Riemannian metric is an example of a distributional metric in this sense. With a view to defining a metric connection in this generality, recall first the Koszul formula which uniquely determines the Levi–Civita connection of a smooth metric $g$
-Riemannian metric is an example of a distributional metric in this sense. With a view to defining a metric connection in this generality, recall first the Koszul formula which uniquely determines the Levi–Civita connection of a smooth metric $g$![]() on $M$
on $M$![]() (cf. [Reference O'Neill33, Ch. 3]):
(cf. [Reference O'Neill33, Ch. 3]):
For a distributional metric $g$![]() , we may use the right-hand side of (3.6) to define a bilinear map $\mathfrak {X}(M)\times \mathfrak {X}(M) \to \mathcal {D}'\mathcal {T}^0_1(M)$
, we may use the right-hand side of (3.6) to define a bilinear map $\mathfrak {X}(M)\times \mathfrak {X}(M) \to \mathcal {D}'\mathcal {T}^0_1(M)$![]() ,
,
called the distributional Levi–Civita connection of $g$![]() ([Reference LeFloch and Mardare27, Def. 4.2]). Note, however, that this is not (yet) a distributional connection in the sense of definition 3.1 since it is of order $(0,\,1)$
([Reference LeFloch and Mardare27, Def. 4.2]). Note, however, that this is not (yet) a distributional connection in the sense of definition 3.1 since it is of order $(0,\,1)$![]() instead of $(1,\,0)$
instead of $(1,\,0)$![]() . In addition to the standard product rules, it also satisfies (the analogues of properties (D4) and (D5) in [Reference O'Neill33, Th. 3.11])
. In addition to the standard product rules, it also satisfies (the analogues of properties (D4) and (D5) in [Reference O'Neill33, Th. 3.11])

for all $X,\, Y,\, Z\in \mathfrak {X}(M)$![]() .
.
In order to obtain an $L^2_{\mathrm {loc}}$![]() -connection from $\nabla ^\flat$
-connection from $\nabla ^\flat$![]() (which then will allow us to define the curvature tensors via definition 3.2), we want to raise the index via $g$
(which then will allow us to define the curvature tensors via definition 3.2), we want to raise the index via $g$![]() , i.e.
, i.e.
To be able to do this, we need to restrict to metrics of higher regularity. It turns out that the Geroch–Traschen class of metrics is a reasonable family of metrics where this strategy can be implemented. This class consists of metrics in $H^1_{\mathrm {loc}}(M) \cap L^\infty _{\mathrm {loc}}(M)$![]() that are uniformly non-degenerate in the sense that $|\det g(F_i,\,F_j)|$
that are uniformly non-degenerate in the sense that $|\det g(F_i,\,F_j)|$![]() is locally bounded away from zero for any local frame $F_i$
is locally bounded away from zero for any local frame $F_i$![]() , see [Reference LeFloch and Mardare27, Prop. 4.4]. For such metrics, hence in particular for any $C^1$
, see [Reference LeFloch and Mardare27, Prop. 4.4]. For such metrics, hence in particular for any $C^1$![]() -Riemannian metric, (3.9) defines an $L^2_{\mathrm {loc}}$
-Riemannian metric, (3.9) defines an $L^2_{\mathrm {loc}}$![]() -connection in the sense of definition 3.1, which therefore has well-defined distributional curvature tensors.
-connection in the sense of definition 3.1, which therefore has well-defined distributional curvature tensors.
Let us analyse the case of a $C^1$![]() -Riemannian metric in more detail, as it will be the most relevant setting in this paper. For such a $g$
-Riemannian metric in more detail, as it will be the most relevant setting in this paper. For such a $g$![]() and $X,\,Y\in \mathfrak {X}(M)$
and $X,\,Y\in \mathfrak {X}(M)$![]() , $\nabla _X Y$
, $\nabla _X Y$![]() is in fact a continuous vector field, so $\nabla$
is in fact a continuous vector field, so $\nabla$![]() is a $C^0$
is a $C^0$![]() -connection, implying that $(R(X,\,Y)Z)(\theta ) \in \mathcal {D}'{}^{(1)}(M)$
-connection, implying that $(R(X,\,Y)Z)(\theta ) \in \mathcal {D}'{}^{(1)}(M)$![]() . Consequently, $R\in \mathcal {D}'{}^{(1)}\mathcal {T}^1_3(M)$
. Consequently, $R\in \mathcal {D}'{}^{(1)}\mathcal {T}^1_3(M)$![]() .
.
Given $W,\,X,\,Y,\,Z \in \mathfrak {X}(M)$![]() , we then define $R(W,\,X,\,Y,\,Z)\in \mathcal {D}'{}^{(1)}$
, we then define $R(W,\,X,\,Y,\,Z)\in \mathcal {D}'{}^{(1)}$![]() by
by
Then using (3.3), (3.4) and (3.8), it follows that (cf. [Reference LeFloch and Mardare27, Rem. 4.5])
This identity can also be verified using local coordinates since there is a well-defined multiplication of distributions of first order with $C^1$![]() -functions.
-functions.
The Ricci tensor of a $C^1$![]() -Riemannian metric $g$
-Riemannian metric $g$![]() is given by (3.5), and will be denoted by $\mathrm {Ric}_g$
is given by (3.5), and will be denoted by $\mathrm {Ric}_g$![]() or $\mathrm {Ric}(g)$
or $\mathrm {Ric}(g)$![]() . Alternatively, it can be calculated in terms of $g$
. Alternatively, it can be calculated in terms of $g$![]() -orthonormal frames (which are only $C^1$
-orthonormal frames (which are only $C^1$![]() ): Note that (3.4) remains valid even when $Y$
): Note that (3.4) remains valid even when $Y$![]() and $\theta$
and $\theta$![]() are only $C^1$
are only $C^1$![]() , so $(\nabla _X(\nabla _Y Z))(\theta ) \in \mathcal {D}'{}^{(1)}(M)$
, so $(\nabla _X(\nabla _Y Z))(\theta ) \in \mathcal {D}'{}^{(1)}(M)$![]() ($X\in \mathfrak {X}(M)$
($X\in \mathfrak {X}(M)$![]() ). Given a smooth local frame $F_i$
). Given a smooth local frame $F_i$![]() with dual frame $F^j$
with dual frame $F^j$![]() , by (3.5) we have $\mathrm {Ric}(X,\,Y) = (R(X,\,F_i)Y)(F^i)$
, by (3.5) we have $\mathrm {Ric}(X,\,Y) = (R(X,\,F_i)Y)(F^i)$![]() . If now $E_i\in \mathfrak {X}_{C^1}(U)$
. If now $E_i\in \mathfrak {X}_{C^1}(U)$![]() is a local $g$
is a local $g$![]() -orthonormal frame, $g(E_i,\,E_j)=\delta _{ij}$
-orthonormal frame, $g(E_i,\,E_j)=\delta _{ij}$![]() and we set $E^i:=g(E_i,\,.\,) \in \Omega ^1_{C^1}(U)$
and we set $E^i:=g(E_i,\,.\,) \in \Omega ^1_{C^1}(U)$![]() . Expressing $F^i,\, F_i$
. Expressing $F^i,\, F_i$![]() as $C^1$
as $C^1$![]() -linear combinations of $E^i,\, E_i$
-linear combinations of $E^i,\, E_i$![]() , then by what was said above, we may calculate as in the smooth case to arrive at
, then by what was said above, we may calculate as in the smooth case to arrive at
where the scalar product is now between the $C^1$![]() -vector field $E_i$
-vector field $E_i$![]() and the $\mathcal {D}'{}^{(1)}$
and the $\mathcal {D}'{}^{(1)}$![]() -vector field $R(E_i,\,X)Y$
-vector field $R(E_i,\,X)Y$![]() . Finally, again by the above observations, the standard local formulae hold in $\mathcal {D}'{}^{(1)}$
. Finally, again by the above observations, the standard local formulae hold in $\mathcal {D}'{}^{(1)}$![]() :
:

Turning now to Ricci curvature bounds, recall ([Reference Schwartz35, Ch. I, §4]) that a distribution $T\in \mathcal {D}'(U)$![]() ($U\subseteq \mathbb {R}^n$
($U\subseteq \mathbb {R}^n$![]() open) is called non-negative, $T\ge 0$
open) is called non-negative, $T\ge 0$![]() , if $T(\varphi )\equiv \langle T,\,\varphi \rangle \ge 0$
, if $T(\varphi )\equiv \langle T,\,\varphi \rangle \ge 0$![]() for each test function $\varphi \ge 0$
for each test function $\varphi \ge 0$![]() . In the manifold context, we therefore call $T\in \mathcal {D}'(M)$
. In the manifold context, we therefore call $T\in \mathcal {D}'(M)$![]() non-negative if $T(\omega ) \equiv \langle T, \omega \rangle \ge 0$
non-negative if $T(\omega ) \equiv \langle T, \omega \rangle \ge 0$![]() for any compactly supported non-negative one-density $\omega$
for any compactly supported non-negative one-density $\omega$![]() . Any such distribution is in fact of order $0$
. Any such distribution is in fact of order $0$![]() , hence is a measure on $M$
, hence is a measure on $M$![]() . For $S,\, T\in \mathcal {D}'(M)$
. For $S,\, T\in \mathcal {D}'(M)$![]() we say that $S\ge T$
we say that $S\ge T$![]() if $S-T\ge 0$
if $S-T\ge 0$![]() . Following [Reference Graf14, Def. 3.3], we say that a $C^1$
. Following [Reference Graf14, Def. 3.3], we say that a $C^1$![]() -Riemannian metric $g$
-Riemannian metric $g$![]() satisfies $\mathrm {Ric} \ge K$
satisfies $\mathrm {Ric} \ge K$![]() for some $K\in \mathbb {R}$
for some $K\in \mathbb {R}$![]() if
if
where the inequality is in $\mathcal {D}'{}^{(1)}(M) \subset \mathcal {D}'(M)$![]() , as explained above. Upper bounds are defined analogously.
, as explained above. Upper bounds are defined analogously.
In our analysis of distributional curvature bounds, a main tool will be regularization via convolution. To accomodate the manifold setting, we employ a construction from [Reference Grosser, Kunzinger, Oberguggenberger and Steinbauer17, 3.2.10], [Reference Kunzinger, Steinbauer, Stojković and Vickers23, Sec. 2], [Reference Graf14, Sec. 3.3]). Let $\rho \in \mathcal {D}(B_1(0))$![]() (with $B_1(0)$
(with $B_1(0)$![]() the unit ball in $\mathbb {R}^n$
the unit ball in $\mathbb {R}^n$![]() ), $\int \rho = 1$
), $\int \rho = 1$![]() , $\rho \ge 0$
, $\rho \ge 0$![]() and, for $\varepsilon \in (0,\,1]$
and, for $\varepsilon \in (0,\,1]$![]() , set $\rho _{\varepsilon }(x):=\varepsilon ^{-n}\rho (\frac {x}{\varepsilon })$
, set $\rho _{\varepsilon }(x):=\varepsilon ^{-n}\rho (\frac {x}{\varepsilon })$![]() . Pick a countable and locally finite family of relatively compact chart neighbourhoods $(U_i,\,\psi _i)$
. Pick a countable and locally finite family of relatively compact chart neighbourhoods $(U_i,\,\psi _i)$![]() ($i\in \mathbb {N}$
($i\in \mathbb {N}$![]() ), as well as a subordinate partition of unity $(\zeta _i)_i$
), as well as a subordinate partition of unity $(\zeta _i)_i$![]() with $\mathrm {supp}(\zeta _i)\Subset U_i$
with $\mathrm {supp}(\zeta _i)\Subset U_i$![]() for all $i$
for all $i$![]() . Moreover, choose a family of cut-off functions $\chi _i\in \mathscr {D}(U_i)$
. Moreover, choose a family of cut-off functions $\chi _i\in \mathscr {D}(U_i)$![]() with $\chi _i\equiv 1$
with $\chi _i\equiv 1$![]() on a neighbourhood of $\mathrm {supp}(\zeta _i)$
on a neighbourhood of $\mathrm {supp}(\zeta _i)$![]() . Denote by $f_*$
. Denote by $f_*$![]() (respectively $f^*$
(respectively $f^*$![]() ) the push-forward (resp. pull-back) of a distribution under a diffeomorphism $f$
) the push-forward (resp. pull-back) of a distribution under a diffeomorphism $f$![]() , and set, for any $T \in \mathcal {D}'\mathcal {T}^r_s(M)$
, and set, for any $T \in \mathcal {D}'\mathcal {T}^r_s(M)$![]() ,
,
where the convolution of tensor fields on open subsets of $\mathbb {R}^n$![]() is to be understood component-wise. Due to the presence of the cut-off functions $\chi _i$
is to be understood component-wise. Due to the presence of the cut-off functions $\chi _i$![]() , the map $(\varepsilon,\,x) \mapsto \mathcal {T}\star _M \rho _\varepsilon (x)$
, the map $(\varepsilon,\,x) \mapsto \mathcal {T}\star _M \rho _\varepsilon (x)$![]() is smooth on $(0,\,1] \times M$
is smooth on $(0,\,1] \times M$![]() . Note that, for any compact set $K\Subset M$
. Note that, for any compact set $K\Subset M$![]() , there exists an $\varepsilon _K$
, there exists an $\varepsilon _K$![]() such that for all $\varepsilon <\varepsilon _K$
such that for all $\varepsilon <\varepsilon _K$![]() and all $x\in K$
and all $x\in K$![]() (3.12) is in fact a finite sum with all $\chi _i\equiv 1$
(3.12) is in fact a finite sum with all $\chi _i\equiv 1$![]() . More precisely, this is the case whenever $\varepsilon _K$
. More precisely, this is the case whenever $\varepsilon _K$![]() is less than the distance between the support of $\zeta _i\circ \psi _i^{-1}$
is less than the distance between the support of $\zeta _i\circ \psi _i^{-1}$![]() and the boundary of $\psi _i(U_i)$
and the boundary of $\psi _i(U_i)$![]() for all $i$
for all $i$![]() with ${U_i\cap K\neq \emptyset}$
with ${U_i\cap K\neq \emptyset}$![]() .
.
This ‘manifold convolution’ has smoothing properties that are closely analogous to those of convolution with a mollifier on open subsets of $\mathbb {R}^n$![]() . In particular, for $T\in \mathcal {D}'\mathcal {T}^r_s(M)$
. In particular, for $T\in \mathcal {D}'\mathcal {T}^r_s(M)$![]() we have
we have
and indeed this convergence is even in $C^k_{\mathrm {loc}}$![]() or $W^{k,p}_{\mathrm {loc}}$
or $W^{k,p}_{\mathrm {loc}}$![]() if $T$
if $T$![]() is contained in these spaces ([Reference Graf14, Prop. 3.5]). Note that since $\rho \ge 0$
is contained in these spaces ([Reference Graf14, Prop. 3.5]). Note that since $\rho \ge 0$![]() , $\star _M$
, $\star _M$![]() preserves non-negativity:
preserves non-negativity:
If $M$![]() is compact and $g$
is compact and $g$![]() is a Riemannian metric of regularity at least $C^0$
is a Riemannian metric of regularity at least $C^0$![]() , then since $g_\varepsilon :=g\star _M \rho _\varepsilon \to g$
, then since $g_\varepsilon :=g\star _M \rho _\varepsilon \to g$![]() uniformly on $M$
uniformly on $M$![]() , $g_\varepsilon$
, $g_\varepsilon$![]() is a smooth Riemannian metric on $M$
is a smooth Riemannian metric on $M$![]() for $\varepsilon$
for $\varepsilon$![]() sufficiently small (which we shall always tacitly assume below).
sufficiently small (which we shall always tacitly assume below).
4. Distributional curvature bounds via regularization
Let $M$![]() be a compact manifold equipped with a distributional Riemannian metric $g$
be a compact manifold equipped with a distributional Riemannian metric $g$![]() . As in § 3, we fix a non-negative mollifier $\rho \in \mathcal {D}(B_1(0))$
. As in § 3, we fix a non-negative mollifier $\rho \in \mathcal {D}(B_1(0))$![]() with $\int \rho = 1$
with $\int \rho = 1$![]() and set $g_\varepsilon := g\star _M \rho _\varepsilon$
and set $g_\varepsilon := g\star _M \rho _\varepsilon$![]() . To begin with, we analyse the relationship between distributional Ricci bounds for $g$
. To begin with, we analyse the relationship between distributional Ricci bounds for $g$![]() and classical (pointwise) Ricci bounds for the approximating smooth Riemannian metrics $g_\varepsilon$
and classical (pointwise) Ricci bounds for the approximating smooth Riemannian metrics $g_\varepsilon$![]() . The key to this analysis are certain versions of Friedrichs’ lemma, which provide improved convergence properties of commutators between differentiation and convolution operators. These turned out to be essential for generalizing classical singularity theorems in Lorentzian geometry to metrics of lower regularity ([Reference Graf14, Reference Graf, Grant, Kunzinger and Steinbauer15, Reference Kunzinger, Ohanyan, Schinnerl and Steinbauer20, Reference Kunzinger, Steinbauer, Stojković and Vickers24, Reference Kunzinger, Steinbauer and Vickers25]). The versions we shall rely on here are the following (see [Reference Graf14, Lem. 4.8, 4.9]):
. The key to this analysis are certain versions of Friedrichs’ lemma, which provide improved convergence properties of commutators between differentiation and convolution operators. These turned out to be essential for generalizing classical singularity theorems in Lorentzian geometry to metrics of lower regularity ([Reference Graf14, Reference Graf, Grant, Kunzinger and Steinbauer15, Reference Kunzinger, Ohanyan, Schinnerl and Steinbauer20, Reference Kunzinger, Steinbauer, Stojković and Vickers24, Reference Kunzinger, Steinbauer and Vickers25]). The versions we shall rely on here are the following (see [Reference Graf14, Lem. 4.8, 4.9]):
Lemma 4.1
(i) Let $a\in C^1(\mathbb {R}^n)$
 , $f\in C^0(\mathbb {R}^n)$
, $f\in C^0(\mathbb {R}^n)$ . Then $(a*\rho _\varepsilon )(f*\rho _\varepsilon ) - (af)*\rho _\varepsilon \to 0$
. Then $(a*\rho _\varepsilon )(f*\rho _\varepsilon ) - (af)*\rho _\varepsilon \to 0$ in $C^1(K)$
in $C^1(K)$ for any compact set $K\subseteq \mathbb {R}^n$
for any compact set $K\subseteq \mathbb {R}^n$ .
.(ii) Let $a,\, a_\varepsilon \in C^1(\mathbb {R}^n)$
 such that $a_\varepsilon \to a$
such that $a_\varepsilon \to a$ in $C^1$
in $C^1$ and such that for each $K$
and such that for each $K$ compact in $\mathbb {R}^n$
compact in $\mathbb {R}^n$ there exists some $c_K$
there exists some $c_K$ such that $\|a-a_\varepsilon \|_{\infty,K} \le c_K\varepsilon$
such that $\|a-a_\varepsilon \|_{\infty,K} \le c_K\varepsilon$ . Then for any $f\in C^0(\mathbb {R}^n)$
. Then for any $f\in C^0(\mathbb {R}^n)$ we have $a_\varepsilon (f*\rho _\varepsilon ) - (af)*\rho _\varepsilon \to 0$
we have $a_\varepsilon (f*\rho _\varepsilon ) - (af)*\rho _\varepsilon \to 0$ in $C^1(K)$
in $C^1(K)$ for any compact set $K\subseteq \mathbb {R}^n$
for any compact set $K\subseteq \mathbb {R}^n$ .
.
Based on this, we can collect the following commutator properties. Note that the convergence claimed in points (i)–(iii) of proposition 4.2 is, in each case, one order of differentiation better than one would expect from the limiting properties of the individual terms.
Proposition 4.2 Let $g$![]() be a $C^1$
be a $C^1$![]() -Riemannian metric on $M$
-Riemannian metric on $M$![]() , $g_\varepsilon := g\star _M \rho _\varepsilon$
, $g_\varepsilon := g\star _M \rho _\varepsilon$![]() , and let $X,\, Y\in \mathfrak {X}(M)$
, and let $X,\, Y\in \mathfrak {X}(M)$![]() . Then
. Then
(i) $\mathrm {Ric}(g\star _M \rho _\varepsilon ) - \mathrm {Ric}(g)\star _M \rho _\varepsilon \to 0$
 in $C^0(M,\,T^0_2M)$
in $C^0(M,\,T^0_2M)$ as $\varepsilon \to 0$
as $\varepsilon \to 0$ .
.(ii) $\mathrm {Ric}_g(X,\,Y)\star _M \rho _\varepsilon - \mathrm {Ric}_{g_\varepsilon }(X,\,Y) \to 0$
 in $C^0(M)$
in $C^0(M)$ as $\varepsilon \to 0$
as $\varepsilon \to 0$ .
.(iii) $g(X,\,Y)\star _M \rho _\varepsilon - g_\varepsilon (X,\,Y) \to 0$
 in $C^2(M)$
in $C^2(M)$ as $\varepsilon \to 0$
as $\varepsilon \to 0$ .
.
Proof. (i) This is shown in (the proof of) [Reference Graf14, Lem. 4.6], so we only outline the argument briefly. Let $(\varphi,\, U)$![]() be any local chart on $M$
be any local chart on $M$![]() . Then writing out the local expressions for $\mathrm {Ric}(g\star _M \rho _\varepsilon )$
. Then writing out the local expressions for $\mathrm {Ric}(g\star _M \rho _\varepsilon )$![]() and $\mathrm {Ric}(g)\star _M \rho _\varepsilon$
and $\mathrm {Ric}(g)\star _M \rho _\varepsilon$![]() , it follows that it suffices to show that, setting $h:= \varphi _*g$
, it follows that it suffices to show that, setting $h:= \varphi _*g$![]() , $h_\varepsilon := \varphi _*g_\varepsilon$
, $h_\varepsilon := \varphi _*g_\varepsilon$![]() :
:
in $C^1$![]() for any compactly supported smooth function $\zeta$
for any compactly supported smooth function $\zeta$![]() and all $i,\,j,\,k,\,l,\,m$
and all $i,\,j,\,k,\,l,\,m$![]() . This in turn follows from lemma 4.1 (ii), together with [Reference Graf14, (4.4)], which shows that $g_\varepsilon ^{-1}$
. This in turn follows from lemma 4.1 (ii), together with [Reference Graf14, (4.4)], which shows that $g_\varepsilon ^{-1}$![]() converges to $g^{-1}$
converges to $g^{-1}$![]() at least at a linear rate in $\varepsilon$
at least at a linear rate in $\varepsilon$![]() .
.
(ii) Writing $R_\varepsilon$![]() for a component function of a chart representation of $\mathrm {Ric}(g\star _M \rho _\varepsilon )$
for a component function of a chart representation of $\mathrm {Ric}(g\star _M \rho _\varepsilon )$![]() and $R$
and $R$![]() for the corresponding one of $\mathrm {Ric}(g)$
for the corresponding one of $\mathrm {Ric}(g)$![]() , the claim reduces to showing that, for any smooth function $h$
, the claim reduces to showing that, for any smooth function $h$![]() we have that $(R\cdot h)*\rho _\varepsilon - R_\varepsilon \cdot h \to 0$
we have that $(R\cdot h)*\rho _\varepsilon - R_\varepsilon \cdot h \to 0$![]() in $C^0$
in $C^0$![]() . Due to (i), this in turn will follow if we can show that
. Due to (i), this in turn will follow if we can show that
in $C^0$![]() . Here, $R$
. Here, $R$![]() is a distribution of order one, hence can locally be written as a derivative of a continuous function, which we schematically write as $R=\partial f$
is a distribution of order one, hence can locally be written as a derivative of a continuous function, which we schematically write as $R=\partial f$![]() , with $f$
, with $f$![]() continuous. By lemma 4.1 (ii), $(f*\rho _\varepsilon )\cdot h - (fh)*\rho _\varepsilon \to 0$
continuous. By lemma 4.1 (ii), $(f*\rho _\varepsilon )\cdot h - (fh)*\rho _\varepsilon \to 0$![]() in $C^1$
in $C^1$![]() , so
, so
in $C^0$![]() . Here, $(f*\rho _\varepsilon )\partial h - (f\partial h)*\rho _\varepsilon \to 0$
. Here, $(f*\rho _\varepsilon )\partial h - (f\partial h)*\rho _\varepsilon \to 0$![]() in $C^0$
in $C^0$![]() , and the remaining terms give the claim (4.1).
, and the remaining terms give the claim (4.1).
(iii) Via chart representations, and schematically writing $g$![]() also for the local components of the metric $g$
also for the local components of the metric $g$![]() , as well as $\partial g$
, as well as $\partial g$![]() for any first-order derivative, the claim reduces to showing that, for $h\in C^\infty$
for any first-order derivative, the claim reduces to showing that, for $h\in C^\infty$![]() , we have $(\partial g\cdot h)*\rho _\varepsilon - (\partial g*\rho _\varepsilon )\cdot h \to 0$
, we have $(\partial g\cdot h)*\rho _\varepsilon - (\partial g*\rho _\varepsilon )\cdot h \to 0$![]() in $C^1$
in $C^1$![]() . Setting $f:=\partial g\in C^0$
. Setting $f:=\partial g\in C^0$![]() ,
,
By [Reference Graf14, (3.7)], $\|h-h*\rho _\varepsilon \|_{\infty,K} \le c_K\varepsilon$![]() for any compact set $K$
for any compact set $K$![]() , and the same is true when replacing $h$
, and the same is true when replacing $h$![]() by $\partial h$
by $\partial h$![]() here. From this, convergence of the difference of the first two terms to $0$
here. From this, convergence of the difference of the first two terms to $0$![]() in $C^1$
in $C^1$![]() is immediate from lemma 4.1 (ii). Finally, convergence to $0$
is immediate from lemma 4.1 (ii). Finally, convergence to $0$![]() in $C^1$
in $C^1$![]() of the remaining difference follows by taking into account [Reference Graf14, Lem. 4.7].
of the remaining difference follows by taking into account [Reference Graf14, Lem. 4.7].
Theorem 4.3 Let $K\in \mathbb {R}$![]() . Then for any $C^1$
. Then for any $C^1$![]() -Riemannian metric $g$
-Riemannian metric $g$![]() on a compact manifold $M$
on a compact manifold $M$![]() , the following are equivalent:
, the following are equivalent:
(i) $\mathrm {Ric}_g \ge K$
 (resp. $\mathrm {Ric}_g \le K$
(resp. $\mathrm {Ric}_g \le K$ ) in the sense of distributions (see (3.11)).
) in the sense of distributions (see (3.11)).(ii) For each $\delta >0$
 there exists some $\varepsilon _0>0$
there exists some $\varepsilon _0>0$ such that $\mathrm {Ric}_{g_\varepsilon } \ge K-\delta$
such that $\mathrm {Ric}_{g_\varepsilon } \ge K-\delta$ (resp. $\mathrm {Ric}_{g_\varepsilon } \le K+\delta$
(resp. $\mathrm {Ric}_{g_\varepsilon } \le K+\delta$ ) for all $\varepsilon \in (0,\,\varepsilon _0)$
) for all $\varepsilon \in (0,\,\varepsilon _0)$ .
.
Proof. It will suffice to prove the case of lower bounds.
(ii)$\Rightarrow$![]() (i): Fix $X\in \mathfrak {X}(M)$
(i): Fix $X\in \mathfrak {X}(M)$![]() . Setting $\delta :=\frac {1}{k}$
. Setting $\delta :=\frac {1}{k}$![]() , by (ii) and proposition 4.2 (iii), we can pick $\varepsilon _k \searrow 0$
, by (ii) and proposition 4.2 (iii), we can pick $\varepsilon _k \searrow 0$![]() such that (with $\mathrm {Ric}_{\varepsilon }:=\mathrm {Ric}_{g_{\varepsilon }}$
such that (with $\mathrm {Ric}_{\varepsilon }:=\mathrm {Ric}_{g_{\varepsilon }}$![]() ) $\mathrm {Ric}_{\varepsilon _k}(X,\,X) \ge (K-\frac {1}{k})g(X,\,X)\star _M \rho _{\varepsilon _k}$
) $\mathrm {Ric}_{\varepsilon _k}(X,\,X) \ge (K-\frac {1}{k})g(X,\,X)\star _M \rho _{\varepsilon _k}$![]() . Then combining proposition 4.2 (ii) with the fact that $\mathrm {Ric}_g(X,\,X)\star _M \rho _\varepsilon \to \mathrm {Ric}_g(X,\,X)$
. Then combining proposition 4.2 (ii) with the fact that $\mathrm {Ric}_g(X,\,X)\star _M \rho _\varepsilon \to \mathrm {Ric}_g(X,\,X)$![]() in $\mathcal {D}'(M)$
in $\mathcal {D}'(M)$![]() , it follows that $\int _M \mathrm {Ric}_{\varepsilon _k}(X,\,X) \omega \to \langle \mathrm {Ric}_g(X,\,X),\,\omega \rangle$
, it follows that $\int _M \mathrm {Ric}_{\varepsilon _k}(X,\,X) \omega \to \langle \mathrm {Ric}_g(X,\,X),\,\omega \rangle$![]() for any $\omega \in \Gamma _c(M,\,\mathrm {Vol}(M))$
for any $\omega \in \Gamma _c(M,\,\mathrm {Vol}(M))$![]() . If $\omega \ge 0$
. If $\omega \ge 0$![]() , then
, then
Letting $k\to \infty$![]() shows that $\langle \mathrm {Ric}_{g}(X,\,X) - Kg(X,\,X), \omega \rangle \ge 0$
shows that $\langle \mathrm {Ric}_{g}(X,\,X) - Kg(X,\,X), \omega \rangle \ge 0$![]() , as claimed.
, as claimed.
(i)$\Rightarrow$![]() (ii): We may without loss of generality assume that $M$
(ii): We may without loss of generality assume that $M$![]() possesses a global $g$
possesses a global $g$![]() -orthonormal frame $X_1,\,\dots,\,X_n\in \mathfrak {X}(M)$
-orthonormal frame $X_1,\,\dots,\,X_n\in \mathfrak {X}(M)$![]() (otherwise cover $M$
(otherwise cover $M$![]() by finitely many chart domains and argue separately). Due to proposition 4.2 (ii), given $\delta >0$
by finitely many chart domains and argue separately). Due to proposition 4.2 (ii), given $\delta >0$![]() , there exists some $\varepsilon _1>0$
, there exists some $\varepsilon _1>0$![]() such that for $\varepsilon \in (0,\,\varepsilon _1)$
such that for $\varepsilon \in (0,\,\varepsilon _1)$![]() we have
we have

for all $x\in M$![]() and all $(\lambda _1,\,\dots,\,\lambda _n)\in \mathbb {R}^n$
and all $(\lambda _1,\,\dots,\,\lambda _n)\in \mathbb {R}^n$![]() with $\sum _i \lambda _i^2 = 1$
with $\sum _i \lambda _i^2 = 1$![]() . Since the $\lambda _i$
. Since the $\lambda _i$![]() are independent of $x$
are independent of $x$![]() , by definition of $\star _M$
, by definition of $\star _M$![]() (see (3.12)), we may interchange $\sum \lambda _i$
(see (3.12)), we may interchange $\sum \lambda _i$![]() and $\star _M$
and $\star _M$![]() here. Thus, setting $V:=\sum _i \lambda _i X_i$
here. Thus, setting $V:=\sum _i \lambda _i X_i$![]() , (4.2) means that
, (4.2) means that
for any $x\in M$![]() and any $(\lambda _1,\,\dots,\,\lambda _n)\in \mathbb {R}^n$
and any $(\lambda _1,\,\dots,\,\lambda _n)\in \mathbb {R}^n$![]() as above. Analogously, it follows from proposition 4.2 (iii) that there exists some $0<\varepsilon _0\le \varepsilon _1$
as above. Analogously, it follows from proposition 4.2 (iii) that there exists some $0<\varepsilon _0\le \varepsilon _1$![]() such that for any $\varepsilon \in (0,\,\varepsilon _0)$
such that for any $\varepsilon \in (0,\,\varepsilon _0)$![]() and for any such choice of vector field $V$
and for any such choice of vector field $V$![]() , we have
, we have
uniformly on $M$![]() . By assumption, $\mathrm {Ric}_{g}(V,\,V) - Kg(V,\,V) \ge 0$
. By assumption, $\mathrm {Ric}_{g}(V,\,V) - Kg(V,\,V) \ge 0$![]() in $\mathcal {D}'(M)$
in $\mathcal {D}'(M)$![]() , hence (3.14) implies that $\mathrm {Ric}_g(V,\,V)\star _M \rho _\varepsilon - K g(V,\,V)\star _M \rho _\varepsilon \ge 0$
, hence (3.14) implies that $\mathrm {Ric}_g(V,\,V)\star _M \rho _\varepsilon - K g(V,\,V)\star _M \rho _\varepsilon \ge 0$![]() . Consequently,
. Consequently,
This same inequality then holds for each individual $g$![]() -unit vector $V$
-unit vector $V$![]() in any $T_xM$
in any $T_xM$![]() . Finally, since $g_\varepsilon \to g$
. Finally, since $g_\varepsilon \to g$![]() uniformly on the $g$
uniformly on the $g$![]() -unit tangent bundle, by making $\varepsilon _0$
-unit tangent bundle, by making $\varepsilon _0$![]() smaller once more we may replace $(-2\delta /3) g(V,\,V)$
smaller once more we may replace $(-2\delta /3) g(V,\,V)$![]() by $-\delta g_\varepsilon (V,\,V)$
by $-\delta g_\varepsilon (V,\,V)$![]() on the right-hand side of (4.4), thereby concluding the proof.
on the right-hand side of (4.4), thereby concluding the proof.
Remark 4.4 The arguments used to prove proposition 4.2 and theorem 4.3 in fact do not depend on the particular form of the Ricci tensor. Analogous characterizations of distributional curvature bounds via regularizations therefore also hold for other curvature quantities, in particular for sectional curvature bounds.
5. From distributional to synthetic lower Ricci bounds
In this section, we show that if $M$![]() is a compact manifold with a $C^1$
is a compact manifold with a $C^1$![]() -Riemannian metric that has $K\in \mathbb {R}$
-Riemannian metric that has $K\in \mathbb {R}$![]() as a lower distributional Ricci curvature bound, then the associated metric measure space satisfies the corresponding bound on its $\infty$
as a lower distributional Ricci curvature bound, then the associated metric measure space satisfies the corresponding bound on its $\infty$![]() -Ricci curvature in the sense of [Reference Lott and Villani28]. Let us first recall the basic notions and definitions, following [Reference Lott and Villani28, Reference Villani40]. For any Polish space $(X,\,d)$
-Ricci curvature in the sense of [Reference Lott and Villani28]. Let us first recall the basic notions and definitions, following [Reference Lott and Villani28, Reference Villani40]. For any Polish space $(X,\,d)$![]() and probability measures $\mu,\, \nu \in P(X)$
and probability measures $\mu,\, \nu \in P(X)$![]() denote by $W_2(\mu,\,\nu )$
denote by $W_2(\mu,\,\nu )$![]() the Wasserstein distance of order $2$
the Wasserstein distance of order $2$![]() between $\mu$
between $\mu$![]() and $\nu$
and $\nu$![]() (cf. [Reference Villani40, Def. 6.1]), i.e.
(cf. [Reference Villani40, Def. 6.1]), i.e.

The space of probability measures $\mu$![]() such that $\int _X d(x_0,\,x)^2\, d\mu (x) < \infty$
such that $\int _X d(x_0,\,x)^2\, d\mu (x) < \infty$![]() for some (hence any) $x_0\in X$
for some (hence any) $x_0\in X$![]() , equipped with the metric $W_2$
, equipped with the metric $W_2$![]() , is called the Wasserstein space of order $2$
, is called the Wasserstein space of order $2$![]() , and is denoted by $P_2(X)$
, and is denoted by $P_2(X)$![]() . We will henceforth always assume that $X$
. We will henceforth always assume that $X$![]() is compact. In the case we are mainly interested in, $X=M$
is compact. In the case we are mainly interested in, $X=M$![]() will be a compact Riemannian manifold. We then write $P^{\mathrm {ac}}_2(X)$
will be a compact Riemannian manifold. We then write $P^{\mathrm {ac}}_2(X)$![]() for the subspace of $P_2(X)$
for the subspace of $P_2(X)$![]() of those measures that are absolutely continuous with respect to the Riemannian volume density $d\mathrm {vol}_g$
of those measures that are absolutely continuous with respect to the Riemannian volume density $d\mathrm {vol}_g$![]() .
.
Given a continuous convex function $U:[0,\,\infty ) \to \mathbb {R}$![]() with $U(0)=0$
with $U(0)=0$![]() and $\nu \in P(X)$
and $\nu \in P(X)$![]() , define $U_\nu : P_2(X) \to \mathbb {R}\cup \{\infty \}$
, define $U_\nu : P_2(X) \to \mathbb {R}\cup \{\infty \}$![]() by
by
Here, $\mu =\rho \nu + \mu _s$![]() is the Lebesgue decomposition of $\mu$
is the Lebesgue decomposition of $\mu$![]() with respect to $\nu$
with respect to $\nu$![]() into the absolutely continuous part $\rho \nu$
into the absolutely continuous part $\rho \nu$![]() and the singular part $\mu _s$
and the singular part $\mu _s$![]() , and $U'(\infty ) := \lim _{r\to \infty } U(r)/r$
, and $U'(\infty ) := \lim _{r\to \infty } U(r)/r$![]() . The space of all functions $U$
. The space of all functions $U$![]() as above such that additionally the function $\psi (\lambda ):=e^{\lambda }U(e^{-\lambda })$
as above such that additionally the function $\psi (\lambda ):=e^{\lambda }U(e^{-\lambda })$![]() is convex on $\mathbb {R}$
is convex on $\mathbb {R}$![]() is denoted by $\mathcal {DC}_\infty$
is denoted by $\mathcal {DC}_\infty$![]() . The only example of an element of $\mathcal {DC}_\infty$
. The only example of an element of $\mathcal {DC}_\infty$![]() that we shall make use of is $U_\infty (r):= r\log r$
that we shall make use of is $U_\infty (r):= r\log r$![]() . Using these notions, we now can give the following definition ([Reference Lott and Villani28, Def. 0.7]):
. Using these notions, we now can give the following definition ([Reference Lott and Villani28, Def. 0.7]):
Definition 5.1 A compact measured length space $(X,\,d,\,\nu )$![]() (with $\nu$
(with $\nu$![]() a probability measure) has $\infty$
a probability measure) has $\infty$![]() -Ricci curvature bounded below by $K\in \mathbb {R}$
-Ricci curvature bounded below by $K\in \mathbb {R}$![]() if for all $\mu _0,\,\mu _1\in P_2(X)$
if for all $\mu _0,\,\mu _1\in P_2(X)$![]() with $\mathrm {supp}(\mu _0)\subseteq \mathrm {supp}(\nu )$
with $\mathrm {supp}(\mu _0)\subseteq \mathrm {supp}(\nu )$![]() and $\mathrm {supp}(\mu _1)\subseteq \mathrm {supp}(\nu )$
and $\mathrm {supp}(\mu _1)\subseteq \mathrm {supp}(\nu )$![]() , there exists a Wasserstein geodesic $\{\mu _t\}_{t\in [0,1]}$
, there exists a Wasserstein geodesic $\{\mu _t\}_{t\in [0,1]}$![]() from $\mu _0$
from $\mu _0$![]() to $\mu _1$
to $\mu _1$![]() such that for all $U\in \mathcal {DC}_\infty$
such that for all $U\in \mathcal {DC}_\infty$![]() and all $t\in [0,\,1]$
and all $t\in [0,\,1]$![]() , we have
, we have
Here, the function $\lambda _K$![]() is defined as follows: Let $p(r):=rU_+'(r) - U(r)$
is defined as follows: Let $p(r):=rU_+'(r) - U(r)$![]() , $p(0)=0$
, $p(0)=0$![]() , then $\lambda _K(U):=\inf _{r>0} K {p(r)}/{r}$
, then $\lambda _K(U):=\inf _{r>0} K {p(r)}/{r}$![]() (see [Reference Lott and Villani28, Def. 5.13]).
(see [Reference Lott and Villani28, Def. 5.13]).
This property is called weak displacement convexity. We note that in the case of $U_\infty$![]() , we obtain $\lambda _K(U_\infty ) = K$
, we obtain $\lambda _K(U_\infty ) = K$![]() .
.
For $(M,\,g)$![]() , a compact connected Riemannian manifold with volume form $d\mathrm {vol}_g$
, a compact connected Riemannian manifold with volume form $d\mathrm {vol}_g$![]() , letting
, letting
and denoting by $d_g$![]() the Riemannian distance induced by $g$
the Riemannian distance induced by $g$![]() , [Reference Lott and Villani28, Th. 0.12, Th. 7.3] implies:
, [Reference Lott and Villani28, Th. 0.12, Th. 7.3] implies:
Theorem 5.2 Let $M$![]() be a compact connected manifold with a Riemannian metric $g$
be a compact connected manifold with a Riemannian metric $g$![]() of regularity $C^2$
of regularity $C^2$![]() . Then the measured length space $(M,\,d_g,\,\nu _g)$
. Then the measured length space $(M,\,d_g,\,\nu _g)$![]() has $\infty$
has $\infty$![]() -Ricci curvature bounded below by $K\in \mathbb {R}$
-Ricci curvature bounded below by $K\in \mathbb {R}$![]() if and only if $\mathrm {Ric}_g \ge Kg$
if and only if $\mathrm {Ric}_g \ge Kg$![]() .
.
Let now $g$![]() be a Riemannian metric of regularity $C^1$
be a Riemannian metric of regularity $C^1$![]() on the compact manifold $M$
on the compact manifold $M$![]() , and let $g_\varepsilon := g\star _M \rho _\varepsilon$
, and let $g_\varepsilon := g\star _M \rho _\varepsilon$![]() be as in (3.12). We first study the convergence of the measured length spaces $(M,\,d_{g_\varepsilon },\,\mathrm {vol}_{g_\varepsilon })$
be as in (3.12). We first study the convergence of the measured length spaces $(M,\,d_{g_\varepsilon },\,\mathrm {vol}_{g_\varepsilon })$![]() towards $(M,\,d_g,\,d\mathrm {vol}_g)$
towards $(M,\,d_g,\,d\mathrm {vol}_g)$![]() :
:
Proposition 5.3 Let $M$![]() be a compact connected manifold with a $C^0$
be a compact connected manifold with a $C^0$![]() -Riemannian metric $g$
-Riemannian metric $g$![]() , and let $g_\varepsilon = g\star _M \rho _\varepsilon$
, and let $g_\varepsilon = g\star _M \rho _\varepsilon$![]() . Then $(M,\,d_{g_\varepsilon },\,\mathrm {vol}_{g_\varepsilon }) \to (M,\,d_g,\,d\mathrm {vol}_g)$
. Then $(M,\,d_{g_\varepsilon },\,\mathrm {vol}_{g_\varepsilon }) \to (M,\,d_g,\,d\mathrm {vol}_g)$![]() in the measured Gromov–Hausdorff sense.
in the measured Gromov–Hausdorff sense.
Proof. Since $g_\varepsilon \to g$![]() uniformly on $M$
uniformly on $M$![]() , for any $\delta >0$
, for any $\delta >0$![]() , there exists some $\varepsilon _0>0$
, there exists some $\varepsilon _0>0$![]() such that for any $\varepsilon \in (0,\,\varepsilon _0)$
such that for any $\varepsilon \in (0,\,\varepsilon _0)$![]() , we have
, we have
Moreover, also by uniform convergence, $\mathrm {vol}_{g_\varepsilon }(M) \to \mathrm {vol}_{g}(M)$![]() . The claim therefore follows from [Reference Allen and Sormani1, Th. 1.2].
. The claim therefore follows from [Reference Allen and Sormani1, Th. 1.2].
Using this result, we can now show:
Theorem 5.4 Let $M$![]() be a compact connected manifold with a $C^1$
be a compact connected manifold with a $C^1$![]() -Riemannian metric $g$
-Riemannian metric $g$![]() that satisfies $\mathrm {Ric}_g \ge Kg$
that satisfies $\mathrm {Ric}_g \ge Kg$![]() in the distributional sense (see (3.11)). Then $(X,\,d_g,\,\nu _g)$
in the distributional sense (see (3.11)). Then $(X,\,d_g,\,\nu _g)$![]() has $\infty$
has $\infty$![]() -Ricci curvature bounded below by $K$
-Ricci curvature bounded below by $K$![]() .
.
Proof. Fix $\delta >0$![]() . By theorem 4.3, there exists some $\varepsilon _0>0$
. By theorem 4.3, there exists some $\varepsilon _0>0$![]() such that, for any $0<\varepsilon <\varepsilon _0$
such that, for any $0<\varepsilon <\varepsilon _0$![]() , the smooth metric $g_\varepsilon$
, the smooth metric $g_\varepsilon$![]() satisfies $\mathrm {Ric}_{g_\varepsilon } \ge (K-\delta ) g_\varepsilon$
satisfies $\mathrm {Ric}_{g_\varepsilon } \ge (K-\delta ) g_\varepsilon$![]() . Furthermore, proposition 5.3 shows that $(M,\,d_{g_\varepsilon },\,\nu _{g_\varepsilon }) \to (M,\,d_g,\,\nu _g)$
. Furthermore, proposition 5.3 shows that $(M,\,d_{g_\varepsilon },\,\nu _{g_\varepsilon }) \to (M,\,d_g,\,\nu _g)$![]() in the measured Gromov–Hausdorff sense. Also, due to theorem 5.2, each $(M,\,d_{g_\varepsilon },\,\nu _{g_\varepsilon })$
in the measured Gromov–Hausdorff sense. Also, due to theorem 5.2, each $(M,\,d_{g_\varepsilon },\,\nu _{g_\varepsilon })$![]() has $\infty$
has $\infty$![]() -Ricci curvature bounded below by $K-\delta$
-Ricci curvature bounded below by $K-\delta$![]() . We may now employ the stability of weak displacement convexity [Reference Lott and Villani28, Th. 4.15] to conclude that for any $U\in \mathcal {DC}_\infty$
. We may now employ the stability of weak displacement convexity [Reference Lott and Villani28, Th. 4.15] to conclude that for any $U\in \mathcal {DC}_\infty$![]() , $U_{\nu _g}$
, $U_{\nu _g}$![]() is weakly $\lambda _{K-\delta }$
is weakly $\lambda _{K-\delta }$![]() -displacement convex. Since this holds for any $\delta >0$
-displacement convex. Since this holds for any $\delta >0$![]() , the claim follows.
, the claim follows.
6. From synthetic to distributional lower Ricci bounds
We now turn to the converse of the implication considered previously. When trying to infer distributional Ricci bounds from synthetic ones, one faces significantly greater technical difficulties. Indeed one can observe that when deriving classical bounds for smooth (at least $C^2$![]() -) Riemannian metrics from synthetic ones, the standard proofs (e.g. [Reference Lott and Villani28, Th. 7.3], [Reference von Renesse and Sturm41, Th. 1.1]) make use of analytic tools that cease to be available in regularities strictly below $C^2$
-) Riemannian metrics from synthetic ones, the standard proofs (e.g. [Reference Lott and Villani28, Th. 7.3], [Reference von Renesse and Sturm41, Th. 1.1]) make use of analytic tools that cease to be available in regularities strictly below $C^2$![]() , e.g. Jacobi fields, or estimates of curvature quantities along geodesics, both of which would require the evaluation of curvature terms (which are, at best, only defined almost everywhere) along curves, hence along null sets. Our strategy will again be to work with regularized smooth metrics $g_\varepsilon = g\star _M \rho _\varepsilon$
, e.g. Jacobi fields, or estimates of curvature quantities along geodesics, both of which would require the evaluation of curvature terms (which are, at best, only defined almost everywhere) along curves, hence along null sets. Our strategy will again be to work with regularized smooth metrics $g_\varepsilon = g\star _M \rho _\varepsilon$![]() , and we will assume the metric $g$
, and we will assume the metric $g$![]() itself to be of class $C^{1,1}$
itself to be of class $C^{1,1}$![]() (continuously differentiable with Lipschitz continuous first derivatives). This regularity class has turned out to be of considerable interest in applications to general relativity, since it still guarantees, on the one hand, unique solvability of the geodesic equations, and local boundedness of all curvature quantities (cf. [Reference Graf, Grant, Kunzinger and Steinbauer15, Reference Kunzinger, Steinbauer, Stojković and Vickers24, Reference Kunzinger, Steinbauer and Vickers25, Reference Minguzzi31]). From the technical point of view, such metrics still provide enough control over curvature quantities of the approximating metrics $g_\varepsilon$
(continuously differentiable with Lipschitz continuous first derivatives). This regularity class has turned out to be of considerable interest in applications to general relativity, since it still guarantees, on the one hand, unique solvability of the geodesic equations, and local boundedness of all curvature quantities (cf. [Reference Graf, Grant, Kunzinger and Steinbauer15, Reference Kunzinger, Steinbauer, Stojković and Vickers24, Reference Kunzinger, Steinbauer and Vickers25, Reference Minguzzi31]). From the technical point of view, such metrics still provide enough control over curvature quantities of the approximating metrics $g_\varepsilon$![]() to suitably adapt arguments from the smooth setting.
to suitably adapt arguments from the smooth setting.
Suppose that $g$![]() is a $C^{1,1}$
is a $C^{1,1}$![]() -Riemannian metric on a compact connected manifold $M$
-Riemannian metric on a compact connected manifold $M$![]() such that $\mathrm {Ric}_g$
such that $\mathrm {Ric}_g$![]() does not have $K$
does not have $K$![]() as a lower distributional bound. By theorem 4.3, this means that for some $\delta >0$
as a lower distributional bound. By theorem 4.3, this means that for some $\delta >0$![]() there exists a sequence $\varepsilon _k \searrow 0$
there exists a sequence $\varepsilon _k \searrow 0$![]() and vectors $v_k \in T_{x_k}M$
and vectors $v_k \in T_{x_k}M$![]() , such that
, such that
Henceforth, we write $g_k$![]() for $g_{\varepsilon _k}$
for $g_{\varepsilon _k}$![]() . By compactness, we may suppose that $x_k \to x_0$
. By compactness, we may suppose that $x_k \to x_0$![]() , $v_k\to v$
, $v_k\to v$![]() , $v\in T_{x_0}M$
, $v\in T_{x_0}M$![]() . For later use, we note that (6.1) remains true if we multiply $v_k$
. For later use, we note that (6.1) remains true if we multiply $v_k$![]() by a constant, so that by re-scaling we may assume the norms of $v_k$
by a constant, so that by re-scaling we may assume the norms of $v_k$![]() , $v$
, $v$![]() as small as we wish. Our aim in this section is to derive a contradiction to $g$
as small as we wish. Our aim in this section is to derive a contradiction to $g$![]() possessing $K$
possessing $K$![]() as a lower $\infty$
as a lower $\infty$![]() -Ricci bound by constructing a Wasserstein geodesic along which displacement convexity (5.1) fails for the function $U_\infty (r) = r\log r$
-Ricci bound by constructing a Wasserstein geodesic along which displacement convexity (5.1) fails for the function $U_\infty (r) = r\log r$![]() . To this end, we will follow the basic structure of the proof of [Reference Lott and Villani28, Th. 7.3].
. To this end, we will follow the basic structure of the proof of [Reference Lott and Villani28, Th. 7.3].
To begin with, for any $k$![]() , we choose a smooth map $\phi _k:M\to \mathbb {R}$
, we choose a smooth map $\phi _k:M\to \mathbb {R}$![]() such that
such that
as follows: Working in local coordinates centred at $x_0$![]() , we define
, we define
in a neighbourhood of $x_0=0$![]() and extend this function to all of $M$
and extend this function to all of $M$![]() as $\phi _k:=\zeta \cdot \tilde \phi _k$
as $\phi _k:=\zeta \cdot \tilde \phi _k$![]() , where $\zeta$
, where $\zeta$![]() is a plateau function that equals $1$
is a plateau function that equals $1$![]() in a neighbourhood of $x_0$
in a neighbourhood of $x_0$![]() (to be further specified below). Here, ${}^{g_k}\Gamma ^l_{ij}$
(to be further specified below). Here, ${}^{g_k}\Gamma ^l_{ij}$![]() denote the Christoffel symbols of $g_k$
denote the Christoffel symbols of $g_k$![]() in the local coordinates. Clearly, $\phi _k \to \phi = \zeta \tilde \phi$
in the local coordinates. Clearly, $\phi _k \to \phi = \zeta \tilde \phi$![]() in $C^\infty (M)$
in $C^\infty (M)$![]() , where
, where
and we have $\nabla ^{g}\phi (x_0)=-v$![]() and $\mathrm {Hess}^{g}(\phi )(x_0)=0$
and $\mathrm {Hess}^{g}(\phi )(x_0)=0$![]() .
.
As in § 2, let $c(x,\,y):=d(x,\,y)^2/2$![]() , with $d$
, with $d$![]() the Riemannian distance induced by $g$
the Riemannian distance induced by $g$![]() and analogously $c_k(x,\,y):=d_k(x,\,y)^2/2$
and analogously $c_k(x,\,y):=d_k(x,\,y)^2/2$![]() for the metric $g_k$
for the metric $g_k$![]() . We next want to show that there exists some constant $\kappa >0$
. We next want to show that there exists some constant $\kappa >0$![]() such that, if $\|\nabla ^{g_k} \phi _k\|_\infty \le \kappa$
such that, if $\|\nabla ^{g_k} \phi _k\|_\infty \le \kappa$![]() (which can be achieved by making $\|v_k\|_{g_k}$
(which can be achieved by making $\|v_k\|_{g_k}$![]() uniformly small), then $\phi _k$
uniformly small), then $\phi _k$![]() is $c_k$
is $c_k$![]() -concave for each $k\in \mathbb {N}$
-concave for each $k\in \mathbb {N}$![]() . To this end, we employ the following result from [Reference Glaudo13]:
. To this end, we employ the following result from [Reference Glaudo13]:
Theorem 6.1 [Reference Glaudo13, Th. 1.1]
Let $(M,\,g)$![]() be a compact Riemannian manifold with sectional curvature bounded from above by $K\ge 0$
be a compact Riemannian manifold with sectional curvature bounded from above by $K\ge 0$![]() . Then there exists a constant $C_*:=C_*(\mathrm {inj}(M),$
. Then there exists a constant $C_*:=C_*(\mathrm {inj}(M),$![]() $K,\,\mathrm {diam}(M))>0$
$K,\,\mathrm {diam}(M))>0$![]() such that, for any $\varepsilon >0$
such that, for any $\varepsilon >0$![]() , if $\phi \in C^2(M,\,\mathbb {R})$
, if $\phi \in C^2(M,\,\mathbb {R})$![]() satisfies
satisfies
then $\phi$![]() is $c$
is $c$![]() -concave.
-concave.
Thus, to establish the above claim, we need to see that when applying this result to $g_k$![]() , all the quantities used in the estimates can be controlled uniformly in $k$
, all the quantities used in the estimates can be controlled uniformly in $k$![]() . For the injectivity radii $\mathrm {inj}_{g_k}$
. For the injectivity radii $\mathrm {inj}_{g_k}$![]() this follows from [Reference Cheeger, Gromov and Taylor7, Th. 4.7], to the effect that a uniform bound on the Riemann tensor combined with a uniform lower bound on the volumes of distance balls of radius $1$
this follows from [Reference Cheeger, Gromov and Taylor7, Th. 4.7], to the effect that a uniform bound on the Riemann tensor combined with a uniform lower bound on the volumes of distance balls of radius $1$![]() gives a lower bound on the injectivity radius (cf. [Reference Kunzinger, Steinbauer and Stojković22, Th. 3.3] and the discussion following it). Moreover, both the Hessians with respect to $g_k$
gives a lower bound on the injectivity radius (cf. [Reference Kunzinger, Steinbauer and Stojković22, Th. 3.3] and the discussion following it). Moreover, both the Hessians with respect to $g_k$![]() and the $g_k$
and the $g_k$![]() -diameters of $M$
-diameters of $M$![]() converge uniformly, so the claim follows. We henceforth assume that the $\|v_k\|_{g_k}$
converge uniformly, so the claim follows. We henceforth assume that the $\|v_k\|_{g_k}$![]() are sufficiently small to guarantee $c_k$
are sufficiently small to guarantee $c_k$![]() -concavity of $\phi _k$
-concavity of $\phi _k$![]() .
.
Let $\eta _0^{(k)} := \mathrm {vol}_{g_k}(V)^{-1} 1_V$![]() be a uniform distribution on some open neighbourhood $V$
be a uniform distribution on some open neighbourhood $V$![]() of $x_0$
of $x_0$![]() (to be specified more precisely below, but in any case such that $\phi _k = \tilde \phi _k$
(to be specified more precisely below, but in any case such that $\phi _k = \tilde \phi _k$![]() and $\phi = \tilde \phi$
and $\phi = \tilde \phi$![]() on $V$
on $V$![]() ), $\eta _0 := \mathrm {vol}_{g}(V)^{-1} 1_V$
), $\eta _0 := \mathrm {vol}_{g}(V)^{-1} 1_V$![]() , $\mu _0^{(k)} := \eta _0^{(k)} d\mathrm {vol}_{g_k}$
, $\mu _0^{(k)} := \eta _0^{(k)} d\mathrm {vol}_{g_k}$![]() and $\mu _0 := \eta _0 d\mathrm {vol}_{g}$
and $\mu _0 := \eta _0 d\mathrm {vol}_{g}$![]() . Then $\mu _0^{(k)}\ll d\mathrm {vol}_{g_k}$
. Then $\mu _0^{(k)}\ll d\mathrm {vol}_{g_k}$![]() and $\mu _0\ll d\mathrm {vol}_{g}$
and $\mu _0\ll d\mathrm {vol}_{g}$![]() are probability measures. Set $F_t^{(k)}(y):=\exp ^{g_k}_y(-t\nabla ^{g_k} \phi _k)$
are probability measures. Set $F_t^{(k)}(y):=\exp ^{g_k}_y(-t\nabla ^{g_k} \phi _k)$![]() , $F_t(y):=\exp ^{g}_y(-t \nabla ^g \phi )$
, $F_t(y):=\exp ^{g}_y(-t \nabla ^g \phi )$![]() and $F^{(k)} := F_1^{(k)}$
and $F^{(k)} := F_1^{(k)}$![]() , $F := F_1$
, $F := F_1$![]() . Since $\phi _k$
. Since $\phi _k$![]() is $c_k$
is $c_k$![]() -concave, [Reference McCann30, Th. 8] and [Reference Cordero-Erausquin, McCann and Schmuckenschläger9, Cor. 5.2] show that, for each $t\in [0,\,1]$
-concave, [Reference McCann30, Th. 8] and [Reference Cordero-Erausquin, McCann and Schmuckenschläger9, Cor. 5.2] show that, for each $t\in [0,\,1]$![]() , $\mu _t^{(k)} := (F_{t}^{(k)})_\#\mu _0^{(k)}$
, $\mu _t^{(k)} := (F_{t}^{(k)})_\#\mu _0^{(k)}$![]() is a $c_k$
is a $c_k$![]() -optimal transport from $\mu _0^{(k)}$
-optimal transport from $\mu _0^{(k)}$![]() to $\mu _t^{(k)}$
to $\mu _t^{(k)}$![]() . Consequently, $t\mapsto \mu _t^{(k)}$
. Consequently, $t\mapsto \mu _t^{(k)}$![]() is a geodesic for the $2$
is a geodesic for the $2$![]() -Wasserstein distance induced by $g_k$
-Wasserstein distance induced by $g_k$![]() . Furthermore, denoting by $W^{(k)}_2$
. Furthermore, denoting by $W^{(k)}_2$![]() and $W_2$
and $W_2$![]() the Wasserstein distances induced by $d_{g_k}$
the Wasserstein distances induced by $d_{g_k}$![]() and $d_g$
and $d_g$![]() , respectively, (5.3) shows that by picking a subsequence, we may assume without loss of generality that for each $k$
, respectively, (5.3) shows that by picking a subsequence, we may assume without loss of generality that for each $k$![]() we have $(1-1/k)W_2(\mu,\,\nu ) \le W^{(k)}_2(\mu,\,\nu ) \le (1+1/k)W_2(\mu,\,\nu )$
we have $(1-1/k)W_2(\mu,\,\nu ) \le W^{(k)}_2(\mu,\,\nu ) \le (1+1/k)W_2(\mu,\,\nu )$![]() for all $\mu,\, \nu \in P_2(M)$
for all $\mu,\, \nu \in P_2(M)$![]() . Since $P_2(M)$
. Since $P_2(M)$![]() is compact ([Reference Villani40, Rem. 6.19]), we are precisely in the setting of the following auxilliary result:
is compact ([Reference Villani40, Rem. 6.19]), we are precisely in the setting of the following auxilliary result:
Lemma 6.2 Let $(X,\,d)$![]() be a compact metric space and let $d_k$
be a compact metric space and let $d_k$![]() be a sequence of metrics on $X$
be a sequence of metrics on $X$![]() such that, for each $k\in \mathbb {N}$
such that, for each $k\in \mathbb {N}$![]() ,
,
for all $x,\,y,\,\in X$![]() . Let $\gamma _k: [0,\,1] \to X$
. Let $\gamma _k: [0,\,1] \to X$![]() be a $d_k$
be a $d_k$![]() -geodesic. Then there exists a subsequence $(\gamma _{k_l})$
-geodesic. Then there exists a subsequence $(\gamma _{k_l})$![]() of $(\gamma _k)$
of $(\gamma _k)$![]() that converges uniformly to a $d$
that converges uniformly to a $d$![]() -geodesic $\gamma : [0,\,1]\to X$
-geodesic $\gamma : [0,\,1]\to X$![]() with $d$
with $d$![]() -length $L_d(\gamma ) = \lim _{l\to \infty } L_{d_{k_l}}(\gamma _{k_l})$
-length $L_d(\gamma ) = \lim _{l\to \infty } L_{d_{k_l}}(\gamma _{k_l})$![]() .
.
Proof. By compactness, we may suppose that $\gamma _k(0)\to p\in X$![]() and $\gamma _k(1)\to q\in X$
and $\gamma _k(1)\to q\in X$![]() . Also, we may assume the $\gamma _k$
. Also, we may assume the $\gamma _k$![]() to be parametrized proportional to arclength, so $d_k(\gamma _k(s),\,\gamma _k(t)) = d_k(\gamma _k(0),\,\gamma _k(1))|s-t|$
to be parametrized proportional to arclength, so $d_k(\gamma _k(s),\,\gamma _k(t)) = d_k(\gamma _k(0),\,\gamma _k(1))|s-t|$![]() . Then by (6.3) we obtain
. Then by (6.3) we obtain
for $k$![]() large and any $s,\,t\in [0,\,1]$
large and any $s,\,t\in [0,\,1]$![]() , showing that $(\gamma _k)_k$
, showing that $(\gamma _k)_k$![]() is uniformly equicontinuous, and pointwise bounded as $X$
is uniformly equicontinuous, and pointwise bounded as $X$![]() is compact. The existence of a uniformly convergent subsequence therefore follows from the Arzela–Ascoli theorem. For simplicity, we denote this subsequence again by $(\gamma _k)_k$
is compact. The existence of a uniformly convergent subsequence therefore follows from the Arzela–Ascoli theorem. For simplicity, we denote this subsequence again by $(\gamma _k)_k$![]() .
.
Next, fix $\varepsilon >0$![]() and denote by $\sigma = \{t_0=0 < \dots < t_{n_\sigma }=1\}$
and denote by $\sigma = \{t_0=0 < \dots < t_{n_\sigma }=1\}$![]() any subdivision of the interval $[0,\,1]$
any subdivision of the interval $[0,\,1]$![]() , then there exists some $k_0 = k_0(\varepsilon,\,\sigma )$
, then there exists some $k_0 = k_0(\varepsilon,\,\sigma )$![]() such that for $k\ge k_0$
such that for $k\ge k_0$![]() we have
we have

Consequently,

Letting $\varepsilon \to 0$![]() and taking the supremum over all $\sigma$
and taking the supremum over all $\sigma$![]() , we obtain $d(\gamma (0),\,\gamma (1)) = L_d(\gamma )$
, we obtain $d(\gamma (0),\,\gamma (1)) = L_d(\gamma )$![]() . Finally, $L_{d_k}(\gamma _k) = d_k(\gamma _k(0),\,\gamma _k(1)) \to d(\gamma (0),\,\gamma (1)) = L_d(\gamma )$
. Finally, $L_{d_k}(\gamma _k) = d_k(\gamma _k(0),\,\gamma _k(1)) \to d(\gamma (0),\,\gamma (1)) = L_d(\gamma )$![]() .
.
Thus, up to picking another subsequence, we conclude that $\mu _t^{(k)}$![]() converges to a $W_2$
converges to a $W_2$![]() -geodesic $\chi _t$
-geodesic $\chi _t$![]() . Since $\sqrt {\det {g_k}} \to \sqrt {\det {g}}$
. Since $\sqrt {\det {g_k}} \to \sqrt {\det {g}}$![]() uniformly on $M$
uniformly on $M$![]() and $\mathrm {vol}_{g_k}(V)\to \mathrm {vol}_g(V)$
and $\mathrm {vol}_{g_k}(V)\to \mathrm {vol}_g(V)$![]() , by [Reference Villani40, Th. 6.9] $\mu _0^{(k)} \to \mu _0$
, by [Reference Villani40, Th. 6.9] $\mu _0^{(k)} \to \mu _0$![]() in $W_2$
in $W_2$![]() . From the above, it therefore follows that, in particular, $\chi _1$
. From the above, it therefore follows that, in particular, $\chi _1$![]() is an optimal transport of $\mu _0$
is an optimal transport of $\mu _0$![]() , hence by theorem 2.3 is of the form $\chi _1 = T_\#\mu _0$
, hence by theorem 2.3 is of the form $\chi _1 = T_\#\mu _0$![]() , where $T(y) = \exp _y( -\nabla \psi (y))$
, where $T(y) = \exp _y( -\nabla \psi (y))$![]() for some $c$
for some $c$![]() -concave function $\psi : M\to \mathbb {R}$
-concave function $\psi : M\to \mathbb {R}$![]() . Note that henceforth we will often simply write $\exp$
. Note that henceforth we will often simply write $\exp$![]() instead of $\exp ^g$
instead of $\exp ^g$![]() , $\nabla$
, $\nabla$![]() instead of $\nabla ^g$
instead of $\nabla ^g$![]() , etc.
, etc.
We wish to relate this function $\psi$![]() to the limiting function $\phi$
to the limiting function $\phi$![]() from above. To this end, we will make use of results on the strong differentiability of the exponential map of a $C^{1,1}$
from above. To this end, we will make use of results on the strong differentiability of the exponential map of a $C^{1,1}$![]() -metric over the zero-section of $TM$
-metric over the zero-section of $TM$![]() ([Reference Minguzzi31, Th. 3]). Denote by $E$
([Reference Minguzzi31, Th. 3]). Denote by $E$![]() the map, defined on a neighbourhood of $M\times \{0\}$
the map, defined on a neighbourhood of $M\times \{0\}$![]() in $TM$
in $TM$![]() , which maps $(y,\,w)$
, which maps $(y,\,w)$![]() to $(y,\,\exp _y(w))$
to $(y,\,\exp _y(w))$![]() . By [Reference Minguzzi31, Th. 3], $E$
. By [Reference Minguzzi31, Th. 3], $E$![]() is strongly differentiable in any point in $M\times \{0\}$
is strongly differentiable in any point in $M\times \{0\}$![]() . In particular, choosing, as above, local coordinates such that $x_0=0$
. In particular, choosing, as above, local coordinates such that $x_0=0$![]() , the strong differential of $E$
, the strong differential of $E$![]() in $(0,\,0)$
in $(0,\,0)$![]() is given by
is given by
Indeed, the estimate given below [Reference Minguzzi31, (39)] shows that, for $\max (\|y\|,\,\|z\|,\,\|v\|,\,\|w\|) < \delta$![]() , $\delta$
, $\delta$![]() sufficiently small, we have
sufficiently small, we have
Here, $h(\delta )\to 0$![]() as $\delta \to 0$
as $\delta \to 0$![]() . We pick $\delta >0$
. We pick $\delta >0$![]() such that $h(\delta )<1/4$
such that $h(\delta )<1/4$![]() . Now $F_t(y) = \mathrm {pr}_2\circ E(y,\,t\nabla \phi (y))$
. Now $F_t(y) = \mathrm {pr}_2\circ E(y,\,t\nabla \phi (y))$![]() , and rescaling $v$
, and rescaling $v$![]() suitably we can assume that $\|\nabla \phi (y)\|,\, \|\nabla \phi (z)\| \le \delta$
suitably we can assume that $\|\nabla \phi (y)\|,\, \|\nabla \phi (z)\| \le \delta$![]() and $\|D^2\phi \|_\infty \le 1/2$
and $\|D^2\phi \|_\infty \le 1/2$![]() , so that $\|\nabla \phi (y) - \nabla \phi (z)\| \le \frac {1}{2} \|y-z\|$
, so that $\|\nabla \phi (y) - \nabla \phi (z)\| \le \frac {1}{2} \|y-z\|$![]() for $y,\, z$
for $y,\, z$![]() in a $\delta$
in a $\delta$![]() -ball around $0$
-ball around $0$![]() . Then (6.4) gives
. Then (6.4) gives
Thus,
for all $t\in [0,\,1]$![]() . By the choices made above, this entails
. By the choices made above, this entails
It follows that there exists a neighbourhood of $x_0$![]() on which, for any $t\in [0,\,1]$
on which, for any $t\in [0,\,1]$![]() , $F_t$
, $F_t$![]() is a bi-Lipschitz homeomorphism. We note that the same calculation can be carried out for each $F^{(k)}_t$
is a bi-Lipschitz homeomorphism. We note that the same calculation can be carried out for each $F^{(k)}_t$![]() , and in fact both $\delta$
, and in fact both $\delta$![]() and $h(\delta )$
and $h(\delta )$![]() can be chosen uniformly for all $F^{(k)}_t$
can be chosen uniformly for all $F^{(k)}_t$![]() and $F_t$
and $F_t$![]() since they only depend on the bounds on the Christoffel symbols and the Lipschitz constants for the exponential maps (cf. [Reference Minguzzi31, (27), (28), (33)]), all of which are uniformly controlled since $g\in C^{1,1}$
since they only depend on the bounds on the Christoffel symbols and the Lipschitz constants for the exponential maps (cf. [Reference Minguzzi31, (27), (28), (33)]), all of which are uniformly controlled since $g\in C^{1,1}$![]() .
.
From here, the standard change-of-variables formula for bi-Lipschitz maps implies that given a measure $\xi _0 d\mathrm {vol}_g$![]() , its push-forward under $F_t$
, its push-forward under $F_t$![]() possesses a density with respect to $d\mathrm {vol}_g$
possesses a density with respect to $d\mathrm {vol}_g$![]() , namely the map
, namely the map

An analogous equation holds for each $F_t^{(k)}$![]() . We also note that due to the uniform bound we have on the Lipschitz constants of the $g_k$
. We also note that due to the uniform bound we have on the Lipschitz constants of the $g_k$![]() -exponential maps, it follows directly from the proofs of the main theorem in [Reference Leach26] and that of [Reference Minguzzi31, Th. 3] that the inverses of $F_t$
-exponential maps, it follows directly from the proofs of the main theorem in [Reference Leach26] and that of [Reference Minguzzi31, Th. 3] that the inverses of $F_t$![]() and $F_t^{(k)}$
and $F_t^{(k)}$![]() are defined on a neighbourhood of $F_t(x_0)$
are defined on a neighbourhood of $F_t(x_0)$![]() resp. $F_t^{(k)}(x_0)$
resp. $F_t^{(k)}(x_0)$![]() whose size is independent of $t\in [0,\,1]$
whose size is independent of $t\in [0,\,1]$![]() and of $k$
and of $k$![]() . Rescaling the $v_k$
. Rescaling the $v_k$![]() , we may therefore assume that all inverses of the $F_t^{(k)}$
, we may therefore assume that all inverses of the $F_t^{(k)}$![]() are defined on a neighbourhood $\tilde V$
are defined on a neighbourhood $\tilde V$![]() of $x_0=F_0(x_0) =F_0^{(k)}(x_0)$
of $x_0=F_0(x_0) =F_0^{(k)}(x_0)$![]() , and that they converge locally uniformly to $F_t^{-1}$
, and that they converge locally uniformly to $F_t^{-1}$![]() on $\tilde V$
on $\tilde V$![]() (cf. [Reference Barvinek, Daler and Francocircu3]). Finally, we pick a neighbourhood $V$
(cf. [Reference Barvinek, Daler and Francocircu3]). Finally, we pick a neighbourhood $V$![]() of $x_0$
of $x_0$![]() whose image under all $F_t^{(k)}$
whose image under all $F_t^{(k)}$![]() and $F_t$
and $F_t$![]() lies in $\tilde V$
lies in $\tilde V$![]() .
.
Taking this $V$![]() in the definition of $\mu _t^{(k)}$
in the definition of $\mu _t^{(k)}$![]() above, we want to show that the densities of the $\mu _t^{(k)}$
above, we want to show that the densities of the $\mu _t^{(k)}$![]() converge to the density of $\mu _t:=(F_t)_\sharp \mu _0$
converge to the density of $\mu _t:=(F_t)_\sharp \mu _0$![]() . This will require us to uniformly control the functions $\det DF^{(k)}_t$
. This will require us to uniformly control the functions $\det DF^{(k)}_t$![]() from below, a property that will also be needed in a later stage of the proof. We will derive such an estimate by Riccati comparison of the Jacobian differentials of the exponential maps of the $g_k$
from below, a property that will also be needed in a later stage of the proof. We will derive such an estimate by Riccati comparison of the Jacobian differentials of the exponential maps of the $g_k$![]() (cf., e.g. [Reference Dai and Wei10, Sec. 1.5] or [Reference Lott and Villani28, Sec. 7]).
(cf., e.g. [Reference Dai and Wei10, Sec. 1.5] or [Reference Lott and Villani28, Sec. 7]).
Fix some $k\in \mathbb {N}$![]() and, given $y\in M$
and, given $y\in M$![]() , consider the $g_k$
, consider the $g_k$![]() -geodesic $\gamma (t):= F_t^{(k)}(y) = \exp ^{g_k}_y(-t \nabla ^{g_k}\phi _k(y))$
-geodesic $\gamma (t):= F_t^{(k)}(y) = \exp ^{g_k}_y(-t \nabla ^{g_k}\phi _k(y))$![]() . Also, let $e_i$
. Also, let $e_i$![]() be a $g_k$
be a $g_k$![]() -orthonormal basis at $y$
-orthonormal basis at $y$![]() , parallelly transported along $\gamma$
, parallelly transported along $\gamma$![]() . Let $J_i$
. Let $J_i$![]() be the Jacobi-field
be the Jacobi-field
along $\gamma$![]() . Then $J_i(0)=e_i$
. Then $J_i(0)=e_i$![]() and $J_i'(0)= \mathrm {Hess}^{g_k}(\phi _k)_y(e_i)$
and $J_i'(0)= \mathrm {Hess}^{g_k}(\phi _k)_y(e_i)$![]() . Setting $J_{ij}:= \langle J_i, e_j \rangle _{g_k}$
. Setting $J_{ij}:= \langle J_i, e_j \rangle _{g_k}$![]() , the matrix $J:=(J_{ij})$
, the matrix $J:=(J_{ij})$![]() satisfies the initial value problem
satisfies the initial value problem
Here, $K_{ij}(t) = \langle R^{g_k}(e_i(t),\,\dot \gamma (t))\dot \gamma (t), e_j(t) \rangle _{g_k(\gamma (t))}$![]() . Let $U(t) := J'(t)\cdot J^{-1}(t)$
. Let $U(t) := J'(t)\cdot J^{-1}(t)$![]() , $\mathcal {J}(t) := \det J(t) = \det DF^{(k)}_t(y)$
, $\mathcal {J}(t) := \det J(t) = \det DF^{(k)}_t(y)$![]() , and
, and
Then,
and $U$![]() satisfies the matrix Riccati equation (cf. [Reference Dai and Wei10, (1.5.2)])
satisfies the matrix Riccati equation (cf. [Reference Dai and Wei10, (1.5.2)])
with initial condition $U(0) = \mathrm {Hess}^{g_k}(\phi _k)_y$![]() . Since $g\in C^{1,1}$
. Since $g\in C^{1,1}$![]() , $K$
, $K$![]() is bounded, independently of $k$
is bounded, independently of $k$![]() (cf. proposition 4.2 and remark 4.4), so there exists some constant $H>0$
(cf. proposition 4.2 and remark 4.4), so there exists some constant $H>0$![]() such that
such that
in the sense of symmetric bilinear forms. Consider now the comparison equations

with identical initial condition $U_H(0) = U_{-H}(0) = U(0)$![]() . The main theorem of [Reference Eschenburg and Heintze11] then implies that
. The main theorem of [Reference Eschenburg and Heintze11] then implies that
on any common existence interval $[0,\,\bar t]$![]() of $U_H$
of $U_H$![]() , $U_{-H}$
, $U_{-H}$![]() .
.
To solve the comparison equations, it suffices to take a $g_k$![]() -orthogonal matrix $T$
-orthogonal matrix $T$![]() that diagonalizes the initial condition. Then $\tilde U_H := T^{-1}U_HT$
that diagonalizes the initial condition. Then $\tilde U_H := T^{-1}U_HT$![]() solves the same equation, but with diagonal initial conditions, hence the system decouples and can be solved explicitly, namely $\tilde U_H(t) = \mathrm {diag}(s_H^{1}(t),\,\dots,\,s_H^n(t))$
solves the same equation, but with diagonal initial conditions, hence the system decouples and can be solved explicitly, namely $\tilde U_H(t) = \mathrm {diag}(s_H^{1}(t),\,\dots,\,s_H^n(t))$![]() , $\tilde U_{-H}(t) = \mathrm {diag}(s_{-H}^{1}(t),\,\dots,\,s_{-H}^n(t))$
, $\tilde U_{-H}(t) = \mathrm {diag}(s_{-H}^{1}(t),\,\dots,\,s_{-H}^n(t))$![]() for smooth functions $s_{H}^{i}$
for smooth functions $s_{H}^{i}$![]() , $s_{-H}^{i}$
, $s_{-H}^{i}$![]() on $[0,\,\bar t]$
on $[0,\,\bar t]$![]() , given by
, given by

Transforming back it follows that
on $[0,\,\bar t]$![]() . Consequently,
. Consequently,
on $[0,\,\bar t]$![]() , which in turn implies a uniform bound on $h(t)$
, which in turn implies a uniform bound on $h(t)$![]() , independently of $k$
, independently of $k$![]() .
.
We conclude that, in particular,
Hence, also $\det DF^{(k)}_t(y))$![]() is uniformly bounded below. From the explicit form of $F_t^{(k)}$
is uniformly bounded below. From the explicit form of $F_t^{(k)}$![]() it follows that, rescaling the $v_k$
it follows that, rescaling the $v_k$![]() by a factor independent of $k$
by a factor independent of $k$![]() , we may assume without loss of generality that $\bar t = 1$
, we may assume without loss of generality that $\bar t = 1$![]() .
.
We now make the following technical assumption (cf. remark 6.5 below for a discussion):
Assumption 6.3 There exists a (Lebesgue-) null set $N\subseteq M$![]() such that, for each $y\in M\setminus N$
such that, for each $y\in M\setminus N$![]() ,
,
uniformly for $t\in [0,\,1]$![]() .
.
Together with the above, (6.5) for $F_t^{(k)}$![]() , and the fact that $\mathrm {vol}_{g_k} \to \mathrm {vol}_g$
, and the fact that $\mathrm {vol}_{g_k} \to \mathrm {vol}_g$![]() uniformly on $M$
uniformly on $M$![]() imply that $\mu _t^{(k)} \to \mu _t$
imply that $\mu _t^{(k)} \to \mu _t$![]() weakly for each $t\in [0,\,1]$
weakly for each $t\in [0,\,1]$![]() . Since, on the other hand, convergence in the Wasserstein sense implies weak convergence, it follows that $\chi _t = \mu _t$
. Since, on the other hand, convergence in the Wasserstein sense implies weak convergence, it follows that $\chi _t = \mu _t$![]() for all $t\in [0,\,1]$
for all $t\in [0,\,1]$![]() .
.
To continue the argument, we now require the validity of the following two standard results also for $C^{1,1}$![]() -Riemannian metrics: First, the proof of [Reference Ambrosio and Gigli2, Cor. 3.22] relies on [Reference Ambrosio and Gigli2, Th. 3.10], which clearly applies to the current setting, as well as on [Reference Ambrosio and Gigli2, Rem. 2.35], which corresponds to our lemma 2.2, so remains true for $g\in C^{1,1}$
-Riemannian metrics: First, the proof of [Reference Ambrosio and Gigli2, Cor. 3.22] relies on [Reference Ambrosio and Gigli2, Th. 3.10], which clearly applies to the current setting, as well as on [Reference Ambrosio and Gigli2, Rem. 2.35], which corresponds to our lemma 2.2, so remains true for $g\in C^{1,1}$![]() . Furthermore, [Reference Cordero-Erausquin, McCann and Schmuckenschläger9, Cor. 5.2] is derived from [Reference Cordero-Erausquin, McCann and Schmuckenschläger9, Lem. 5.1], which carries over verbatim to the $C^{1,1}$
. Furthermore, [Reference Cordero-Erausquin, McCann and Schmuckenschläger9, Cor. 5.2] is derived from [Reference Cordero-Erausquin, McCann and Schmuckenschläger9, Lem. 5.1], which carries over verbatim to the $C^{1,1}$![]() -setting, together with McCann's characterization of optimal transport, which in this regularity takes the form of theorem 2.3, showing that also this result holds for $g\in C^{1,1}$
-setting, together with McCann's characterization of optimal transport, which in this regularity takes the form of theorem 2.3, showing that also this result holds for $g\in C^{1,1}$![]() .
.
Combining these two results, we conclude that with $\psi$![]() the $c$
the $c$![]() -concave function introduced after the proof of lemma 6.2, we have $\chi _t = (H_t)_\sharp \mu _0$
-concave function introduced after the proof of lemma 6.2, we have $\chi _t = (H_t)_\sharp \mu _0$![]() , where $H_t = y\mapsto \exp _y(-t\nabla \psi (y))$
, where $H_t = y\mapsto \exp _y(-t\nabla \psi (y))$![]() . By theorem 2.3 we therefore have, for each $t\in [0,\,1]$
. By theorem 2.3 we therefore have, for each $t\in [0,\,1]$![]() , that $\exp _y(-t\nabla \phi (y)) = \exp _y(-t\nabla \psi (y))$
, that $\exp _y(-t\nabla \phi (y)) = \exp _y(-t\nabla \psi (y))$![]() $\mu _0$
$\mu _0$![]() -almost everywhere and hence Lebesgue-almost everywhere on $V$
-almost everywhere and hence Lebesgue-almost everywhere on $V$![]() . We now again use the fact that by [Reference Minguzzi31, Th. 3], the map $TM\to M\times M$
. We now again use the fact that by [Reference Minguzzi31, Th. 3], the map $TM\to M\times M$![]() , $v_y \mapsto \exp ^g_y(v_y)$
, $v_y \mapsto \exp ^g_y(v_y)$![]() is a bi-Lipschitz homeomorphism on a neighbourhood of the zero-section in $TM$
is a bi-Lipschitz homeomorphism on a neighbourhood of the zero-section in $TM$![]() . For $t>0$
. For $t>0$![]() small, both $t\nabla \phi$
small, both $t\nabla \phi$![]() and $t\nabla \psi$
and $t\nabla \psi$![]() lie in this neighbourhood, hence coincide almost everywhere on $V$
lie in this neighbourhood, hence coincide almost everywhere on $V$![]() . Since, in all further calculations, $\phi$
. Since, in all further calculations, $\phi$![]() enters only via $\nabla \phi$
enters only via $\nabla \phi$![]() , and only measures supported in $V$
, and only measures supported in $V$![]() will be considered, we may without loss of generality henceforth assume that $\phi$
will be considered, we may without loss of generality henceforth assume that $\phi$![]() itself is $c$
itself is $c$![]() -concave. We also note that, by what was said above, $\mu _t$
-concave. We also note that, by what was said above, $\mu _t$![]() is the unique Wasserstein geodesic between $\mu _0$
is the unique Wasserstein geodesic between $\mu _0$![]() and $\mu _1$
and $\mu _1$![]() .
.
Now that we know $c$![]() -concavity of $\phi$
-concavity of $\phi$![]() , we consider more general initial densities $\eta _0$
, we consider more general initial densities $\eta _0$![]() than the constant one we used above. Thus, let $\mu _0=\eta _0 d\mathrm {vol}_g$
than the constant one we used above. Thus, let $\mu _0=\eta _0 d\mathrm {vol}_g$![]() be any probability measure on $V$
be any probability measure on $V$![]() with density $\eta _0$
with density $\eta _0$![]() with respect to $d\mathrm {vol}_g$
with respect to $d\mathrm {vol}_g$![]() . Then since $\phi$
. Then since $\phi$![]() is $c$
is $c$![]() -concave, $\mu _t := (F_t)_\#\mu _0$
-concave, $\mu _t := (F_t)_\#\mu _0$![]() is a $d_g$
is a $d_g$![]() -Wasserstein geodesic, and in fact is the unique geodesic by what was said above. Setting $U \equiv U_\infty = r \log r$
-Wasserstein geodesic, and in fact is the unique geodesic by what was said above. Setting $U \equiv U_\infty = r \log r$![]() , by definition 5.1, we therefore have for all $t\in [0,\,1]$
, by definition 5.1, we therefore have for all $t\in [0,\,1]$![]() :
:
where $\nu$![]() was given in (5.2). As in the proof of [Reference Lott and Villani28, Th. 7.3] (but now using the standard transformation formula for bi-Lipschitz homeomorphisms for $F_t$
was given in (5.2). As in the proof of [Reference Lott and Villani28, Th. 7.3] (but now using the standard transformation formula for bi-Lipschitz homeomorphisms for $F_t$![]() ), we have
), we have
Then setting
and noting that also for $g\in C^{1,1}$![]() we have $W_2(\mu _0,\,\mu _1)^2 = \int _M |\nabla \phi (y)|^2 \eta _0(y)\, d\mathrm {vol}_g(y)$
we have $W_2(\mu _0,\,\mu _1)^2 = \int _M |\nabla \phi (y)|^2 \eta _0(y)\, d\mathrm {vol}_g(y)$![]() , it follows that (6.9) is equivalent to
, it follows that (6.9) is equivalent to

Since this inequality is invariant under non-negative scaling, $\eta _0$![]() can be any non-negative Borel measurable function on $V$
can be any non-negative Borel measurable function on $V$![]() here.
here.
Arguing in a coordinate chart around $x_0$![]() (hence setting $M=\mathbb {R}^n$
(hence setting $M=\mathbb {R}^n$![]() and $x_0=0$
and $x_0=0$![]() for the moment), we now let $\zeta : \mathbb {R}^n\to [0,\,1]$
for the moment), we now let $\zeta : \mathbb {R}^n\to [0,\,1]$![]() be smooth with compact support in the unit ball and $\zeta (0)=1$
be smooth with compact support in the unit ball and $\zeta (0)=1$![]() and set, for $\varepsilon \in (0,\,1]$
and set, for $\varepsilon \in (0,\,1]$![]() , $\eta _{0\varepsilon }(x) := \varepsilon \cdot \zeta (x/\varepsilon )$
, $\eta _{0\varepsilon }(x) := \varepsilon \cdot \zeta (x/\varepsilon )$![]() , and $\eta _{0\varepsilon }^{(k)}(x) := \varepsilon \cdot \zeta ((x-x_k)/\varepsilon )$
, and $\eta _{0\varepsilon }^{(k)}(x) := \varepsilon \cdot \zeta ((x-x_k)/\varepsilon )$![]() . Then
. Then
uniformly in $x$![]() and $\varepsilon$
and $\varepsilon$![]() . Also, setting $C_k(y,\,t) := - \log (\mathrm {vol}_{g_k}(M)) + \log (\det DF^{(k)}_t(y))$
. Also, setting $C_k(y,\,t) := - \log (\mathrm {vol}_{g_k}(M)) + \log (\det DF^{(k)}_t(y))$![]() , (6.7) and (6.8) imply that $|C(y,\,t)-C_k(y,\,t)|$
, (6.7) and (6.8) imply that $|C(y,\,t)-C_k(y,\,t)|$![]() is uniformly bounded in $y,\, t,\, k$
is uniformly bounded in $y,\, t,\, k$![]() and converges pointwise to zero for almost all $y$
and converges pointwise to zero for almost all $y$![]() , uniformly in $t$
, uniformly in $t$![]() , as $k\to \infty$
, as $k\to \infty$![]() . Together with the fact that $\nabla ^{g_k}\phi _k \to \nabla ^g\phi$
. Together with the fact that $\nabla ^{g_k}\phi _k \to \nabla ^g\phi$![]() uniformly on $M$
uniformly on $M$![]() , we conclude that
, we conclude that
as well as

as $k\to \infty$![]() , uniformly in $t\in [0,\,1]$
, uniformly in $t\in [0,\,1]$![]() and in $\varepsilon \in (0,\,1]$
and in $\varepsilon \in (0,\,1]$![]() . Due to (6.10), we conclude that there exists some $k_0$
. Due to (6.10), we conclude that there exists some $k_0$![]() such that, for all $k\ge k_0$
such that, for all $k\ge k_0$![]() , any $\varepsilon \in (0,\,1]$
, any $\varepsilon \in (0,\,1]$![]() and any $t\in [0,\,1]$
and any $t\in [0,\,1]$![]() we have
we have

Letting $\varepsilon \to 0$![]() , the support of $\eta _{0\varepsilon }^{(k)}$
, the support of $\eta _{0\varepsilon }^{(k)}$![]() can be concentrated arbitrarily close to $x_k$
can be concentrated arbitrarily close to $x_k$![]() . The fundamental lemma of the calculus of variations yields that
. The fundamental lemma of the calculus of variations yields that
for all $t\in [0,\,1]$![]() . Using that $|\nabla ^{g_k}\phi _k(x_k)|^2 = g_k(v_k,\,v_k)$
. Using that $|\nabla ^{g_k}\phi _k(x_k)|^2 = g_k(v_k,\,v_k)$![]() and adding $-{1}/{2}(K-{\delta }/{2}) t^2 g_k(v_k,\,v_k)$
and adding $-{1}/{2}(K-{\delta }/{2}) t^2 g_k(v_k,\,v_k)$![]() on both sides of (6.13), we see that the function
on both sides of (6.13), we see that the function
is convex. In particular,
We now note that
To see this, we follow the line of argument in [Reference Lott and Villani28, Lem. 7.4]. Fixing $k$![]() and setting $D(t):= \det ^{\frac {1}{n}}(DF_t^{(k)}(x_k))$
and setting $D(t):= \det ^{\frac {1}{n}}(DF_t^{(k)}(x_k))$![]() , we have $C(t):=C_k(x_k,\,t) = \log (\mathrm {vol}_{g_k}(M)) + n\log (D(t))$
, we have $C(t):=C_k(x_k,\,t) = \log (\mathrm {vol}_{g_k}(M)) + n\log (D(t))$![]() . By [Reference Lott and Villani28, (7.24), (7.30)] and (6.2),
. By [Reference Lott and Villani28, (7.24), (7.30)] and (6.2),
hence
On the other hand, by [Reference Lott and Villani28, (7.16)],
Here, taking $J_i$![]() as in (6.6) (with $y=x_k$
as in (6.6) (with $y=x_k$![]() ), $R(t)$
), $R(t)$![]() is the matrix defined by $J_i'(t) = \sum _j R(t)^j_i J_j(t)$
is the matrix defined by $J_i'(t) = \sum _j R(t)^j_i J_j(t)$![]() . Thus, $R(0)$
. Thus, $R(0)$![]() is the matrix of the $g_k$
is the matrix of the $g_k$![]() -Hessian of $\phi _k$
-Hessian of $\phi _k$![]() at $x_k$
at $x_k$![]() and therefore vanishes by our assumptions (6.2) on $\phi _k$
and therefore vanishes by our assumptions (6.2) on $\phi _k$![]() , which also imply that ${(t\mapsto F_t^{(k)}(x_k))'(0) = v_k}$
, which also imply that ${(t\mapsto F_t^{(k)}(x_k))'(0) = v_k}$![]() . Consequently, (6.17) gives
. Consequently, (6.17) gives
and substituting this into (6.16) proves (6.15).
Finally, combining (6.14) with (6.15) results in
for all $k\ge k_0$![]() , giving the desired contradiction to (6.1). Thus, we arrive at the following result:
, giving the desired contradiction to (6.1). Thus, we arrive at the following result:
Theorem 6.4 Let $M$![]() be a compact connected manifold with a $C^{1,1}$
be a compact connected manifold with a $C^{1,1}$![]() -Riemannian metric $g$
-Riemannian metric $g$![]() such that $(X,\,d_g,\,d\mathrm {vol}_g/\mathrm {vol}_g(M))$
such that $(X,\,d_g,\,d\mathrm {vol}_g/\mathrm {vol}_g(M))$![]() has $\infty$
has $\infty$![]() -Ricci curvature bounded below by $K$
-Ricci curvature bounded below by $K$![]() . Assume further that for some subsequence of $g\star _M \rho _\varepsilon$
. Assume further that for some subsequence of $g\star _M \rho _\varepsilon$![]() , (6.8) is satisfied. Then also $\mathrm {Ric}_g \ge Kg$
, (6.8) is satisfied. Then also $\mathrm {Ric}_g \ge Kg$![]() in the distributional sense.
in the distributional sense.
Remark 6.5 There is a large class of examples of $C^{1,1}$![]() -Riemannian metrics that fail to be $C^2$
-Riemannian metrics that fail to be $C^2$![]() but still satisfy the additional assumption (6.8) in theorem 6.4. Indeed, since the $g_k$
but still satisfy the additional assumption (6.8) in theorem 6.4. Indeed, since the $g_k$![]() are obtained by convolution, for any $C^{1,1}$
are obtained by convolution, for any $C^{1,1}$![]() -metric that is $C^2$
-metric that is $C^2$![]() outside a closed zero set (6.8) clearly holds. In particular, this situation occurs whenever two $C^2$
outside a closed zero set (6.8) clearly holds. In particular, this situation occurs whenever two $C^2$![]() -Riemannian metrics are glued along a closed embedded submanifold of codimension greater or equal than $1$
-Riemannian metrics are glued along a closed embedded submanifold of codimension greater or equal than $1$![]() in such a way that the resulting metric is $C^{1,1}$
in such a way that the resulting metric is $C^{1,1}$![]() .
.
To conclude this paper, let us mention some directions of further research that naturally suggest themselves based on the results derived above. A main question is whether the optimal transport approach and the distributional method cease to produce equivalent lower Ricci curvature bounds when further lowering the regularity of the metric, i.e. if the theories ‘branch’ in the direction of lower differentiability. That this may indeed be the case is supported by two observations: On the one hand, as has also become apparent in § 6, already for $C^{1,1}$![]() metrics one is deprived of many of the standard tools of Riemannian geometry and regularization methods can only partially make up for this loss. Whereas this may be seen as a mere technical inconvenience, it should be taken into account that geometric properties that are taken for granted for $C^2$
metrics one is deprived of many of the standard tools of Riemannian geometry and regularization methods can only partially make up for this loss. Whereas this may be seen as a mere technical inconvenience, it should be taken into account that geometric properties that are taken for granted for $C^2$![]() -metrics in fact cease to hold below this regularity. As examples, we mention the coming apart of the notions of local distance minimizers and geodesics (solutions of the geodesic equation) for $C^{1,\alpha }$
-metrics in fact cease to hold below this regularity. As examples, we mention the coming apart of the notions of local distance minimizers and geodesics (solutions of the geodesic equation) for $C^{1,\alpha }$![]() -metrics ($\alpha \in (0,\,1)$
-metrics ($\alpha \in (0,\,1)$![]() ), cf. [Reference Hartman and Wintner18, Reference Sämann and Steinbauer34], or the more obvious fact that geodesic branching is a generic phenomenon for $C^1$
), cf. [Reference Hartman and Wintner18, Reference Sämann and Steinbauer34], or the more obvious fact that geodesic branching is a generic phenomenon for $C^1$![]() -metrics. It is also an open question whether the well-known equivalence of various entropy conditions (e.g. that of $\mathrm {CD}(K,\,\infty )$
-metrics. It is also an open question whether the well-known equivalence of various entropy conditions (e.g. that of $\mathrm {CD}(K,\,\infty )$![]() with the $\infty$
with the $\infty$![]() -Ricci bounds employed here) continues to hold below $C^2$
-Ricci bounds employed here) continues to hold below $C^2$![]() , i.e. if the synthetic approach itself might branch when lowering the differentiability class of the metric.
, i.e. if the synthetic approach itself might branch when lowering the differentiability class of the metric.
The methods used in this paper are not specifically tied to metrics of Riemannian signature. In fact, our regularization results were derived from constructions that had first been developed in the context of generalizing the classical singularity theorems of general relativity, hence can also be used to analyse metrics of Lorentzian (or indeed arbitrary) signature. Also in this direction, similar questions arise: It has been noted in recent years that a number of standard results of Lorentzian causality theory may lose their validity for metrics of low regularity (and certainly do so below the Lipschitz class), cf., e.g. the phenomenon of ‘bubbling’ metrics ([Reference Chruściel and Grant8, Reference Grant, Kunzinger, Sämann and Steinbauer16]). The Lorentzian synthetic framework [Reference Kunzinger and Sämann21] employed in [Reference Cavalletti and Mondino6] avoids such pathologies explicitly, but at the prize of excluding certain continuous but non-Lipschitz spacetimes from consideration. Finally, it will be of interest to compare the synthetic approach to generalizing the singularity theorems of general relativity ([Reference Cavalletti and Mondino6]) with the distributional one ([Reference Graf14, Reference Graf, Grant, Kunzinger and Steinbauer15, Reference Kunzinger, Ohanyan, Schinnerl and Steinbauer20, Reference Kunzinger, Steinbauer, Stojković and Vickers24, Reference Kunzinger, Steinbauer and Vickers25]).
Acknowledgements
We thank Christian Ketterer for helpful discussions. This work was supported by project P 33594 of the Austrian Science Fund FWF.