Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T02:01:24.504Z Has data issue: false hasContentIssue false
  • English
  • Français

Suspension splittings and James–Hopf invariants

Published online by Cambridge University Press:  30 January 2014

Jelena Grbić ,
Stephen Theriault  and
Jie Wu
Jelena Grbić
Affiliation:
School of Mathematics, University of Manchester, Oxford Road, Manchester M13 9PL, UK
Stephen Theriault
Affiliation:
Department of Mathematical Sciences, University of Aberdeen, Meston Walk, Aberdeen AB24 3UE, UK
Jie Wu
Affiliation:
Department of Mathematics, National University of Singapore, 10 Lower Kent Ridge Road, Singapore 119076, Singapore ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

James constructed a functorial homotopy decomposition 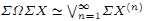for path-connected, p ointed CW-complexes X. We generalize this to a p-local functorial decomposition of ΣA, where A is any functorial retract of a looped co-H-space. This is used to construct Hopf invariants in a more general context. In addition, when A = ΩY is the loops space of a co-H-space, we show that the wedge summands of ΣΩY further functorially decompose by using an action of an appropriate symmetric group. As a valuable example, we give an application to the theory of quasi-symmetric functions.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 144 , Issue 1 , February 2014 , pp. 87 - 108
Copyright
Copyright © Royal Society of Edinburgh 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)