In this paper, we study n-dimensional complete submanifolds with constant scalar curvature in the Euclidean space En+p and n-dimensional compact submanifolds with constant scalar curvature in the unit sphere Sn+p(1). 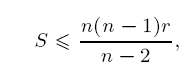We prove that the totally umbilical sphere Sn(r), totally geodesic Euclidean space En and generalized cylinder Sn−1(c) × E1 are the only n-dimensional (n > 2) complete submanifolds Mn with constant scalar curvature n(n − 1)r in the Euclidean space En+p, which satisfy the following condition: where S denotes the squared norm of the second fundamental form of Mn. For compact submanifolds with constant scalar curvature in the unit sphere Sn+p(1), we also obtain a corresponding result (see theorem 1.3).