Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T03:49:47.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Subharmonics near an equilibrium for some second-order Hamiltonian systems

Published online by Cambridge University Press:  14 November 2011

Patricio L. Felmer  and
Elves A. de B. e Silva
Patricio L. Felmer
Affiliation:
Departamento de Ing. Matemática, F.C.F.M., Universidad de Chile, Casilla 170 Correo 3, Santiago, Chile
Elves A. de B. e Silva
Affiliation:
Departamento de Matemática, Universidade Federal de Pernambuco, Cidade Universitária, Recife, Brasil
Get access Rights & Permissions [Opens in a new window]

Synopsis

This work is devoted to the study of subharmonic solutions of a second-order Hamiltonian system

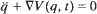
near an equilibrium point, say q = 0. The problem of existence of periodic solutions from the global point of view is also considered.

This problem has been studied for the case where the potential is positive and superquadratic. In this work a potential V that has change in sign is considered. The potential is decomposed as

where P is homogeneous, superquadratic and nondegenerate, and 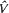is of higher order near 0. In this paper the existence is shown of a sequence of subharmonic solutions of the equation above that converges to the equilibrium, such that their minimal periods converge to infinity.

This problem is approached from a variational point of view. Existence of subharmonic and periodic solutions is obtained via minimax techniques.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 123 , Issue 5 , 1993 , pp. 819 - 834
Copyright
Copyright © Royal Society of Edinburgh 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Benci, V. and Fortunato, D. A Birkhoff–Lewis type result for nonautonomous differential equations. In Partial Differential Equations, (Rio de Janeiro 1986), pp. 85–96, Lecture Notes in Mathematics 1324 (Berlin: Springer, 1988).CrossRefGoogle Scholar
2Benci, V. and Fortunato, D.A ‘Birkhoff-Lewis’ type result for a class of Hamiltonian systems. Manuscripta Math. 59 (1987), 441–456.CrossRefGoogle Scholar
3Birkhoff, G. D. and Lewis, D. C.. On the periodic motion near a given periodic motion of a dynamical system. Ann. Mat. Pura Appl. 12 (1933), 117–133.CrossRefGoogle Scholar
4Felmer, P.. Subharmonics near an equilibrium point for Hamiltonian systems. Manuscripta Math. 66 (1990), 359–396.CrossRefGoogle Scholar
5Han, Z.. Periodic solutions of class of dynamical systems of second order. J. Differential Equations 90(1991), 408–417.CrossRefGoogle Scholar
6Harris, T. C.. Periodic solutions of arbitrary long periods in Hamiltonian systems. J. Differential Equations 4 (1968), 131–141.CrossRefGoogle Scholar
7Lassoued, L.. Periodic solutions of second order superquadratic system with a change of sign in the potential.J. Differential Equations 93 (1991), 1–18.CrossRefGoogle Scholar
8Moser, J.. Proof of a generalized form of a fixed point theorem due to G. D. Birkhoff. Lectures Notes in Mathematics 597 (1977), 464–494.CrossRefGoogle Scholar
9Rabinowitz, P.. On subharmonic solutions of Hamiltonian systems. Comm. Pure Appl. Math. 33 (1980), 609–633.CrossRefGoogle Scholar
10Rabinowitz, P.. Minimax methods in critical point theory with applications to differential equations, C.B.M.S. Regional Conference Series in Mathematics 65 (Providence, RI: American Mathematical Society, 1986).CrossRefGoogle Scholar
11Silva, E.. Linking theorems and applications to semilinear elliptic problems at resonance. Nonlinear Anal. 6 (1990), 455–477.Google Scholar