We study the phenomenon of the infinite-time stabilization of classical global solutions of nonlinear reaction–diffusion equations to an unbounded (singular) stationary state and we present a new case of such an asymptotic singularity pattern formation. We concentrate on the most famous parabolic model, namely the semi-linear Frank-Kamenetskii equation from combustion theory,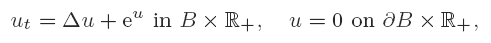where B is a ball in RN. Our goal is to show that a new asymptotic problem arises precisely in dimension 10, not being available in other dimensions (which were studied earlier). For N = 10, we fix the ball B = {|x| < 4} and take bounded initial data u0 below the singular stationary solution Us(x) = ln(16/|x|2), which is unbounded at the origin x = 0.

We establish a sharp estimate on the rate of convergence u(x, t) → Us(x) as t → ∞ on compact subsets bounded away from x = 0 and also at the singularity point. We show that u(0, t) = α0t + O(ln t) → ∞, where the positive constant α0 is given by the first eigenvalue of the associated linear differential operator. We present formal asymptotic results showing that a detailed asymptotic analysis depends on a quite involved balance between various linear and nonlinear terms. Moreover, similar critical asymptotic behaviour is shown to exist in various related nonlinear second- and higher-order parabolic equation.