Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Micheletti, Anna Maria
1994.
A remark on the resonance set for a semilinear elliptic equation.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 124,
Issue. 4,
p.
803.
Pistoia, Angela
1997.
A generic property of the resonance set of an elliptic operator with respect to the domain.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 127,
Issue. 6,
p.
1301.


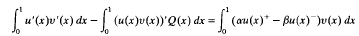
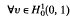 has a nontrivial solution
has a nontrivial solution 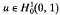 which has exactly one zero in (0,1) and is positive near
which has exactly one zero in (0,1) and is positive near 